
| A. | (0,+∞) | B. | (-∞,$\frac{1}{4}}$) | C. | (${\frac{1}{4}$,+∞) | D. | (0,$\frac{1}{4}}$) |
分析 由f(x)=logc(cx+t)(c>0,c≠1)是“成功函数”,知f(x)在其定义域内为增函数,f(x)=logc(cx+t)=$\frac{1}{2}$x,故cx+t=${c}^{\frac{x}{2}}$,由此能求出t的取值范围.
解答 解:∵f(x)=logc(cx+t)(c>0,c≠1)是“成功函数”,
∴f(x)在其定义域内为增函数,
f(x)=logc(cx+t)=$\frac{1}{2}$x,
∴cx+t=${c}^{\frac{x}{2}}$,
cx-${c}^{\frac{x}{2}}$+t=0,
令a=${c}^{\frac{x}{2}}$>0,
∴a2-a+t=0有两个不同的正数根,
∴$\left\{\begin{array}{l}1-4t>0\\ t>0\end{array}\right.$,
解得t∈(0,$\frac{1}{4}$).
故选:D
点评 本题考查函数的值域的求法,解题的关键是正确理解“成功函数”,解题时要认真审题,仔细解答,注意合理地进行等价转化.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
| 优秀 | 不优秀 | 总计 | |
| 甲队 | 80 | 40 | 120 |
| 乙队 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
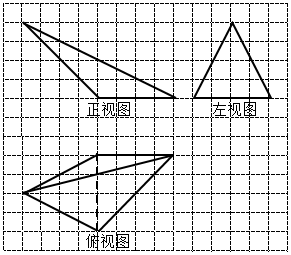 如图,网格纸上每个小正方形的边长均为1,某几何体的三视图如图中粗线所示,则该几何体的所有棱中最长的棱的长度是( )
如图,网格纸上每个小正方形的边长均为1,某几何体的三视图如图中粗线所示,则该几何体的所有棱中最长的棱的长度是( )| A. | 4$\sqrt{6}$ | B. | 2$\sqrt{21}$ | C. | 6 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com