练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若半球内有一内接正方体，则这个半球的表面积与正方体的表面积之比是（　　）
    A．5π：12B．5π：6C．2π：3D．3π：4

    分析 将半球补成整个的球，同时把原半球的内接正方体再补接一同样的正方体，构成的长方体刚好是这个球的内接长方体，那么这个长方体的对角线便是它的外接球的直径．

    解答 解：将半球补成整个的球，同时把原半球的内接正方体再补接一同样的正方体，构成的长方体刚好是这个球的内接长方体，那么这个长方体的对角线便是它的外接球的直径．
    设原正方体棱长为a，球的半径是R，则根据长方体的对角线性质，得（2R）2=a2+a2+（2a）2，
    即4R2=6a2，∴R=$\frac{\sqrt{6}}{2}$a，
    从而S半球的表面积=3πR2=$\frac{9}{2}$πa2，S正方体=6a2，
    因此S半球的表面积：S正方体=3π：4，
    故选：D．

    点评 本题考查球的表面积与正方体的表面积，考查学生的计算能力，正确运用补形法是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．某组合体的三视图如图示，则该组合体的表面积为（　　）
    A．$（6+2\sqrt{2}）π+12$B．8（π+1）C．4（2π+1）D．$（12+2\sqrt{2}）π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．函数y=f（x）的定义域为D，若满足：
    ①f（x）在D内是单调函数；
    ②存在[a，b]⊆D使得f（x）在[a，b]上的值域为[${\frac{a}{2}$，$\frac{b}{2}}$]，则称函数f（x）为“成功函数”．
    若函数f（x）=logc（cx+t）（c＞0，c≠1）是“成功函数”，则t的取值范围为（　　）
    A．（0，+∞）B．（-∞，$\frac{1}{4}}$）C．（${\frac{1}{4}$，+∞）D．（0，$\frac{1}{4}}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在判断“高中生选修文理科是否与性别有关”的一项调查中，通过2×2列联表中的数据计算得到K2≈4.844．已知P（K2≥3.841）≈0.05，P（K2≥5.024）≈0.025，则下列结论正确的是（　　）
    A．认为“选修文理科和性别有关”出错的可能性不超过5%
    B．认为“选修文理科和性别有关”出错的可能性为2.5%
    C．选修文理科和性别有95%的关系
    D．有97.5%的把握认为“选修文理科和性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

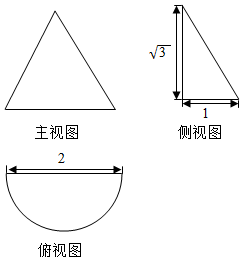    17．某几何体的三视图如图所示，则此几何体的体积为（　　）
    A．$\frac{\sqrt{3}}{6}$πB．$\frac{\sqrt{3}}{3}$πC．$\sqrt{3}$πD．π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．写出等比数列$\frac{8}{3}$，4，6，9，…的通项公式，并写出它的第5项到第8项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=2x2-ax+a2-4，g（x）=x2-x+a2-8，a∈R．
    （1）当a=1时，解不等式f（x）＜0；
    （2）若对任意x＞0，都有f（x）＞g（x）成立，求实数a的取值范围；
    （3）若对任意x1∈[0，1]，总存在x2∈[0，1]，使得不等式f（x1）＞g（x2）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若tanα=$\frac{4}{3}$，则cos2α等于（　　）
    A．$\frac{7}{25}$B．-$\frac{7}{25}$C．1D．$\frac{\sqrt{7}}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=x3-2ax2+3ax，在x=1时取得极值．
    （Ⅰ）求a的值．
    （Ⅱ）若关于x的不等式f（x）-k≤0在[0，4]上恒成立，求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案