
分析 根据条件即可求得点P1,P2到P7的坐标,从而可以求出向量$\stackrel{→}{{P}_{1}{P}_{2}}$,$\stackrel{→}{{P}_{2}{P}_{3}}$,…,$\stackrel{→}{{P}_{6}{P}_{7}}$的坐标,进行向量数量积的坐标运算便可求出a1=1,a2=2,a3=4,a4=8,a5=16,从而便可看出数列{an}是以1为首项,2为公比的等比数列,从而可求出前n项和为2n-1,从而可以得到2n>2017,这样便可判断出最小正整数n的值.
解答 解:由条件得,P1(1,0),P2(1,1),P3(0,2),P4(-2,2),P5(-4,0),P6(-4,-4),P7(0,-8)…;
∴a1=$\stackrel{→}{{P}_{1}{P}_{2}}$•$\stackrel{→}{{P}_{2}{P}_{3}}$=(0,1)•(-1,1)=1,a2=$\stackrel{→}{{P}_{2}{P}_{3}}$•$\stackrel{→}{{P}_{3}{P}_{4}}$=(-1,1)•(-2,0)=2
a3=$\stackrel{→}{{P}_{3}{P}_{4}}$•$\stackrel{→}{{P}_{4}{P}_{5}}$=(-2,0)•(-2,-2)=4,a4=$\stackrel{→}{{P}_{4}{P}_{5}}$•$\stackrel{→}{{P}_{5}{P}_{6}}$=(-2,-2)•(0,-4)=8,
a5=$\stackrel{→}{{P}_{5}{P}_{6}}$•$\stackrel{→}{{P}_{6}{P}_{7}}$=(0,-4)•(4,-4)=16,
∴数列{an}是首项为1,公比为2的等比数列;
∴a1+a2+…+an=$\frac{1•(1-{2}^{n})}{1-2}$=2n-1,
∴由a1+a2+…+an>2016得,2n-1>2016;
∴2n>2017;
∵210=1024,211=2048,
∴满足a1+a2+…+an>2016的最小正整数n=11,
故答案为:11.
点评 本题是一个新定义题目,充分理解题意,并进行相应的转化是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
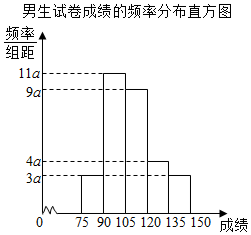 某中学共有4400名学生,其中男生共有2400名,女生2000名,为了解学生的数学基础的差异,采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查,得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表.
某中学共有4400名学生,其中男生共有2400名,女生2000名,为了解学生的数学基础的差异,采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查,得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表.| 成绩分组 | [75,90) | [90,105) | [105,120) | [120,135) | [135,150) |
| 频数 | 2 | 6 | 8 | 7 | b |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 不优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| K0 | 2.706 | 3.841 | 6,635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某组合体的三视图如图示,则该组合体的表面积为( )
某组合体的三视图如图示,则该组合体的表面积为( )| A. | $(6+2\sqrt{2})π+12$ | B. | 8(π+1) | C. | 4(2π+1) | D. | $(12+2\sqrt{2})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC∩BD=O,A1B=A1D=$\sqrt{2}$,AB=AA1=2.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC∩BD=O,A1B=A1D=$\sqrt{2}$,AB=AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 几何体EFG-ABCD的面ABCD,ADGE,DCFG均为矩形,AD=DC=1,AE=$\sqrt{2}$.
几何体EFG-ABCD的面ABCD,ADGE,DCFG均为矩形,AD=DC=1,AE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,$\frac{1}{4}}$) | C. | (${\frac{1}{4}$,+∞) | D. | (0,$\frac{1}{4}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 认为“选修文理科和性别有关”出错的可能性不超过5% | |
| B. | 认为“选修文理科和性别有关”出错的可能性为2.5% | |
| C. | 选修文理科和性别有95%的关系 | |
| D. | 有97.5%的把握认为“选修文理科和性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | 1 | D. | $\frac{\sqrt{7}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com