
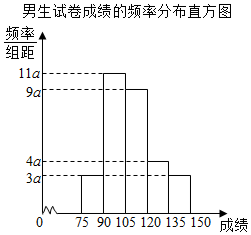
 某中学共有4400名学生,其中男生共有2400名,女生2000名,为了解学生的数学基础的差异,采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查,得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表.
某中学共有4400名学生,其中男生共有2400名,女生2000名,为了解学生的数学基础的差异,采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查,得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表.| 成绩分组 | [75,90) | [90,105) | [105,120) | [120,135) | [135,150) |
| 频数 | 2 | 6 | 8 | 7 | b |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 不优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| K0 | 2.706 | 3.841 | 6,635 |
分析 (1)根据分层抽样的比例,求出a,b的值,以分组的中点数据为平均数,即可估计该校男生和女生的数学成绩;
(2)求出K2,与临界值比较,即可判断是否有90%的把握认为男女生的数学基础有差异.
解答 解:(1)在选取55名同学中,男生有$\frac{2400}{4400}×55$=30人,女生55-30=25人,
由男生试卷成绩的频率分布直方图知道,15×(3a+4a+9a+11a+3a)=1,∴a=$\frac{1}{450}$,
由女生试卷成绩的频数分布表知道,2+6+8+7+b=25,∴b=1,
以分组的中点数据为平均数,该校男生数学成绩=$\frac{1}{30}×(3×82.5+11×97.5+9×112.5+4×127.5+3×142.5)$=109分;
女生的数学成绩=$\frac{1}{25}×(2×82.5+6×97.5+8×112.5+7×127.5+2×142.5)$=113.1分;
(2)2×2列联表
| 男生 | 女生 | 总计 | |
| 优秀 | 7 | 9 | 16 |
| 不优秀 | 23 | 16 | 39 |
| 总计 | 30 | 25 | 55 |
点评 本题主要考查频率分布直方图、频数分布表,考查独立性检验的应用,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于基础题.


科目:高中数学 来源: 题型:选择题
| 感冒 | 不感冒 | 合计 | |
| 男生 | 5 | 27 | 32 |
| 女生 | 9 | 19 | 28 |
| 合计 | 13 | 47 | 60 |
| 参考数据 P(K2≥2.072)≈0.15 P(K2≥2.706)≈0.10 P(K2≥6.635)≈0.010 |
| A. | 在犯错概率不超过10%的前提下认为该班“感冒与性别有关” | |
| B. | 在犯错概率不超过10%的前提下不能认为该班“感冒与性别有关” | |
| C. | 有15%的把握认为该班“感冒与性别有关” | |
| D. | 在犯错概率不超过10%的前提下认为该班“感冒与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
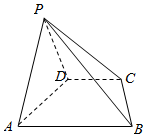 如图,四棱锥中P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°.
如图,四棱锥中P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
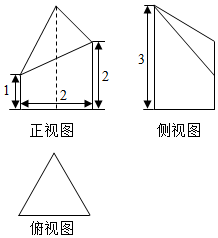
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 不优秀 | 总计 | |
| 甲队 | 80 | 40 | 120 |
| 乙队 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com