练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知棱长为a的正三棱柱ABC-A1B1C1的六个顶点都在半径为$\frac{\sqrt{21}}{6}$的球面上，则a的值为1．

    分析 正三棱柱的底面中心的连线的中点就是外接球的球心，根据球的半径，利用勾股定理建立方程，即可求出a的值

    解答 解：由题意可知：正三棱柱的底面中心的连线的中点就是外接球的球心，底面中心到顶点的距离为：$\frac{\sqrt{3}}{3}$a，
    所以外接球的半径为：$\frac{\sqrt{21}}{6}$=$\sqrt{\frac{{a}^{2}}{4}+\frac{{a}^{2}}{3}}$．
    所以a=1，
    故答案为：1．

    点评 本题是基础题，考查正三棱柱的外接球的半径的求法，找出球的球心是解题的关键，考查空间想象能力，计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．直线y=x-3的倾斜角为45°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

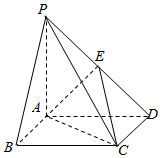    7．如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点，且PA=AD．
    （1）求证：PB∥平面AEC；
    （2）求证：AE⊥平面PCD；
    （3）设二面角D-AE-C为60°，且AP=1，求D到平面AEC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

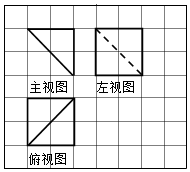
    4．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥与其外接球的体积比是（　　）
    A．$\frac{2\sqrt{3}}{9π}$B．$\frac{\sqrt{3}}{9π}$C．$\frac{\sqrt{2}}{16π}$D．$\frac{8\sqrt{2}}{π}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

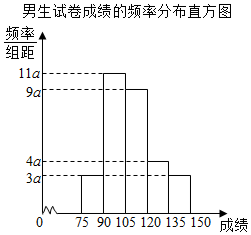    11．某中学共有4400名学生，其中男生共有2400名，女生2000名，为了解学生的数学基础的差异，采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查，得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表．
    女生试卷成绩的频数分布表
     成绩分组[75，90）[90，105）[105，120）[120，135）[135，150）
     频数 2 6 8 7 b
    （1）计算a，b的值，以分组的中点数据为平均数，分别估计该校男生和女生的数学成绩；
    （2）若规定成绩在[120，150]内为数学基础优秀，由以上统计数据填写下面的2×2列联表，并判断是否有90%的把握认为男女生的数学基础有差异．
      男生 女生 总计
     优秀   
     不优秀   
     总计   
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    临界值表：
    P（K2≥k0）0.100.050.01
    K02.7063.8416，635

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知一个正方体的顶点都在同一球面上，若球的半径为$\sqrt{3}$，则该正方体的表面积24．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．如图，网格纸上正方形小格的边长为1（单位：cm），图中粗线画出的是某零件的三视图，则该零件的体积（单位：cm2）为（　　）
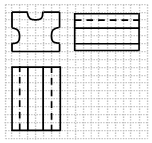
    A．240-24πB．240-12πC．240-8πD．240-4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．如图所示为某几何体的三视图，其体积为48π，则该几何体的表面积为（　　）
    A．24πB．36πC．60πD．78π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知数列{an}满足：a4n-3=1，a4n-1=0，a2n=an，n∈N*，则a2009=1．

    查看答案和解析>>

    同步练习册答案