
【题目】已知函数![]() ,
,![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() 时,若对任意
时,若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,设
,设![]()
![]() ,
,![]() 是
是![]() 的导函数,判断
的导函数,判断![]() 的零点个数,并证明.
的零点个数,并证明.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】分析:(1)由题意,求导,若k≤0,则g′(x)>0,根据函数的单调性即可求得g(x)最大值,即可求得实数k的取值范围;
(2)构造辅助函数,求导,根据函数的单调性及函数零点的判断,即可求得f'(x)的零点个数.
详解: (1)当![]() 时,对任意
时,对任意![]() ,
,![]() 恒成立,
恒成立,
令![]() ,求导
,求导![]() ,
,
由![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,符合题意,
,符合题意,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,![]() ,
,
则![]() 在
在![]() 上是减函数,当
上是减函数,当![]() 时,
时,![]() ,不符合题意,
,不符合题意,
综上可知![]() 的取值范围为
的取值范围为![]() .
.
(2)证明:由题意:![]() ,由此可得
,由此可得![]() 为一个零点,
为一个零点,
令![]() (
(![]() ),则
),则![]() ,
,
![]() 的减区间为
的减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,
其中![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
由零点存在定理及单调性可知在![]() 上存在唯一的零点
上存在唯一的零点![]() ,
,
取![]() ,则
,则![]() ,令
,令![]() ,知
,知![]() 在
在![]() 上是减函数,
上是减函数,
故当![]() 时,
时,![]() ,即
,即![]() ,
,
由零点存在定理及单调性可知在![]() 上存在唯一
上存在唯一![]() ,
,![]() ,
,
由![]() 的单调递减区间是
的单调递减区间是![]() ,则在
,则在![]() 上
上![]() 仅存在唯一的零点
仅存在唯一的零点![]() ,
,
综上可知![]() 共有三个零点.
共有三个零点.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】某面包店随机收集了面包种类的有关数据,经分类整理得到下表:
面包类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
面包个数 | 90 | 60 | 30 | 80 | 100 | 40 |
好评率 | 0.6 | 0.45 | 0.7 | 0.35 | 0.6 | 0.5 |
好评率是指:一类面包中获得好评的个数与该类面包的个数的比值.
(1)从面包店收集的面包中随机选取1个,求这个面包是获得好评的第五类面包的概率;
(2)从面包店收集的面包中随机选取1个,估计这个面包没有获得好评的概率;
(3)面包店为增加利润,拟改变生产策略,这将导致不同类型面包的好评率发生变化.假设表格中只有两类面包的好评率数据发生变化,那么哪类面包的好评率增加0.1,哪类面包的好评率减少0.1,使得获得好评的面包总数与样本中的面包总数的比值达到最大?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() (a>1).
(a>1).
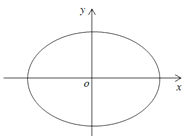
(Ⅰ)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(Ⅱ)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如图频率分布直方图:
五组,并作出如图频率分布直方图:
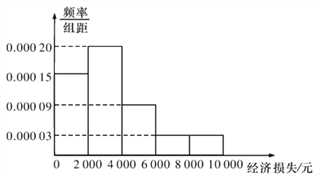
(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过4000元的居民中随机抽取2户进行捐款援助,设抽出损失超过8000元的居民为![]() 户,求
户,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如图,根据图表格中所给数据,分别求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并说明是否有
的值,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 |
|
| |
捐款不超过500元 |
|
| |
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮,中国华为公司研发的![]() 、
、![]() 两种芯片都已获得成功.该公司研发芯片已经耗费资金
两种芯片都已获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产,经市场调查与预测,生产
千万元,现在准备投入资金进行生产,经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() (
(![]() 与
与![]() 都为常数),其图象如图所示.
都为常数),其图象如图所示.
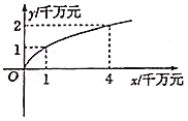
(1)试分别求出生产![]() 、
、![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式;
(千万元)函数关系式;
(2)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() 、
、![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所获利润,当
表示公司所获利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且tan∠EAB=![]() .
.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE,证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
(2)能否在犯错误的概率不超过百分之一的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到定点
到定点![]() 的距离之比它到直线
的距离之比它到直线![]() 的距离小1,设动点
的距离小1,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两个不同的点,过点
两个不同的点,过点![]() 分别作曲线
分别作曲线![]() 的切线,且二者相交于点
的切线,且二者相交于点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求证:![]() ;
;
(3)求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中曲线![]() 的参数方程为
的参数方程为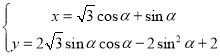 (
(![]() 为参数).若以直角坐标系中的原点
为参数).若以直角坐标系中的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求实数
有公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com