
已知函数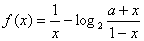 为奇函数.
为奇函数.
(1)求常数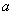 的值;
的值;
(2)判断函数的单调性,并说明理由;
(3)函数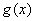 的图象由函数
的图象由函数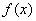 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出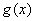 的一个对称中心,若
的一个对称中心,若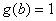 ,求
,求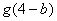 的值。
的值。
科目:高中数学 来源: 题型:
函数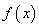 的定义域为D,若对任意
的定义域为D,若对任意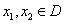 且
且 ,都有
,都有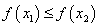 ,则称函数
,则称函数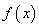 在D上为非减函数,设函数
在D上为非减函数,设函数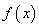 在
在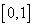 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;②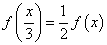 ;③
;③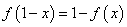 ,则
,则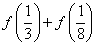 等于( )
等于( )
A.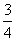 B.
B. 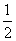 C. 1 D.
C. 1 D.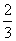
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合M={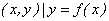 },若对于任意
},若对于任意 ,存在
,存在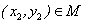 ,使得
,使得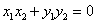 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={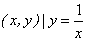 }; ②M={
}; ②M={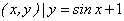 };
};
③M={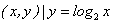 };④M={
};④M={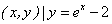 }.
}.
其中是“垂直对点集”的序号是( )
A.①② B.②③ C.①④ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)(x∈N)表示x除以2的余数,函数g(x)(x∈N)表示x除以3的余数,则对任意的x∈N,给出以下式子:
①f(x)≠g(x);②g(2x)=2g(x);③f(2x)=0;④f(x)+f(x+3)=1.其中正确的式子编号是________.(写出所有符合要求的式子编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com