
已知:如图,在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程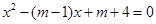 的两根,
的两根,
⑴求a和b的值;
⑵△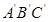 与△ABC开始时完全重合,然后让△ABC固定不动,将
与△ABC开始时完全重合,然后让△ABC固定不动,将
△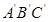 以1厘米/秒的速度沿BC所在的直线向左移动.
以1厘米/秒的速度沿BC所在的直线向左移动.
ⅰ)设x秒后△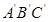 与△ABC 的重叠部分的面积为y平方厘米,求y与x之间的函数关系式,并写出x的取值范围;
与△ABC 的重叠部分的面积为y平方厘米,求y与x之间的函数关系式,并写出x的取值范围;
ⅱ)几秒后重叠部分的面积等于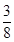 平方厘米?
平方厘米?
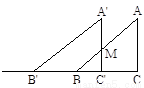
(1) a=4,b=3;(2)经过3秒后重叠部分的面积等于 平方厘米。
平方厘米。
【解析】本试题主要是考查了函数与方程问题,以及三角形的相似的虚拟官职和三角形面积的求解综合运用。
(1)∵△ABC是Rt△且BC=a,AC=b,AB=5 (a>b)
又a、b是方程的两根
∴ 进而分析得到m的值,进而求解得到a,b的值。
进而分析得到m的值,进而求解得到a,b的值。
(2)△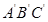 以1厘米/秒的速度沿BC所在直线向左移动。
以1厘米/秒的速度沿BC所在直线向左移动。
∴x秒后BB′=x 则BC′=4-x
∵C′M∥AC ∴△BC′M∽△BCA ∴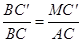 ∴
∴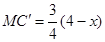
∴ 即
即 ,进而表示得到。
,进而表示得到。
解:(1)∵△ABC是Rt△且BC=a,AC=b,AB=5 (a>b)

又a、b是方程的两根
∴ ∴(a+b)2-2ab=25
∴(a+b)2-2ab=25
(m-1)2-2(m+4)=25 推出 (m-8)(m+4)=0
得m1=8 m2=-4 经检验m=-4(不合舍去) ∴m=8
∴x2-7x+12=0 x1=3 x2=4 ∴a=4,b=3 …………6分
(2) ∵△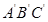 以1厘米/秒的速度沿BC所在直线向左移动。
以1厘米/秒的速度沿BC所在直线向左移动。
∴x秒后BB′=x 则BC′=4-x
∵C′M∥AC ∴△BC′M∽△BCA ∴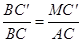 ∴
∴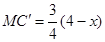
∴ 即
即
∴y=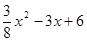 (0
(0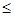 x
x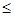 4)
当y=
4)
当y= 时
时
 =
=
解得:x1=3 x2=5(不合舍去)
∴经过3秒后重叠部分的面积等于 平方厘米。
平方厘米。


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
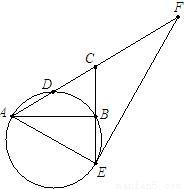
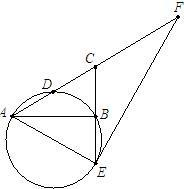 已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.
已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:
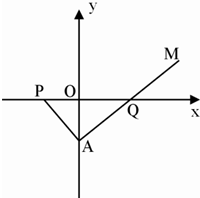 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.查看答案和解析>>
科目:高中数学 来源: 题型:
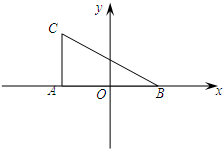 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮复习精练:导数及其应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com