
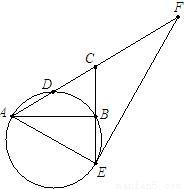
 AC,故有AC=CF,即点C是Rt△AEF的斜边上的中点,有AC=CE,由1中的AE=CE知,AE=CE=AC,故△ACE是等边三角形,∠F=30°,即可求得cosF的值.
AC,故有AC=CF,即点C是Rt△AEF的斜边上的中点,有AC=CE,由1中的AE=CE知,AE=CE=AC,故△ACE是等边三角形,∠F=30°,即可求得cosF的值.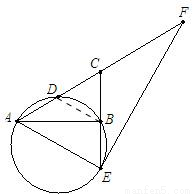 (1)AE=CE;
(1)AE=CE; AC,
AC,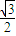 .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
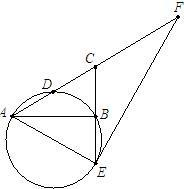 已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.
已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:
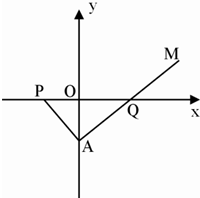 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.查看答案和解析>>
科目:高中数学 来源: 题型:
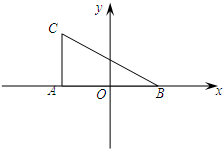 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省蚌埠四校联盟高一自主招生考试数学试卷(解析版) 题型:填空题
已知:如图,在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程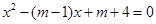 的两根,
的两根,
⑴求a和b的值;
⑵△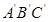 与△ABC开始时完全重合,然后让△ABC固定不动,将
与△ABC开始时完全重合,然后让△ABC固定不动,将
△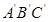 以1厘米/秒的速度沿BC所在的直线向左移动.
以1厘米/秒的速度沿BC所在的直线向左移动.
ⅰ)设x秒后△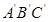 与△ABC 的重叠部分的面积为y平方厘米,求y与x之间的函数关系式,并写出x的取值范围;
与△ABC 的重叠部分的面积为y平方厘米,求y与x之间的函数关系式,并写出x的取值范围;
ⅱ)几秒后重叠部分的面积等于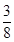 平方厘米?
平方厘米?
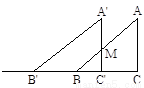
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com