
【题目】已知正项数列{an}满足a1=1,(n+1)a2n+1+an+1an﹣na ![]() =0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
=0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
(1)求{an}和{bn}的通项;
(2)令cn= ![]() , ①求{cn}的前n项和Tn;
, ①求{cn}的前n项和Tn;
②是否存在正整数m满足m>3,c2 , c3 , cm成等差数列?若存在,请求出m;若不存在,请说明理由.
【答案】
(1)解:∵(n+1)a2n+1+an+1an﹣na ![]() =0,∴[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.
=0,∴[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.
∴(n+1)an+1﹣nan=0,解得 ![]() =
= ![]() .
.
∴an= ![]()
![]() …
… ![]() a1=
a1= ![]()
![]() …
… ![]() ×1=
×1= ![]() .
.
∴an= ![]() .
.
∵数列{bn}的前n项和为Sn且Sn=1﹣bn.
∴n≥2时,bn=Sn﹣Sn﹣1=1﹣bn﹣(1﹣bn﹣1),化为:bn= ![]() bn﹣1.
bn﹣1.
n=1时,b1=S1=1﹣b1,解得b1= ![]() .
.
∴数列{bn}是等比数列,首项与公比都为 ![]() .
.
∴bn= ![]()
(2)解:①cn= ![]() =
= ![]() ,
,
∴数列{cn}的前n项和Tn= ![]() +
+ ![]() +…+
+…+ ![]() .
.
∴ ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,
,
可得: ![]() =
= ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= 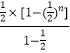 ﹣
﹣ ![]() ,
,
可得:Sn=2﹣ ![]() .
.
②假设存在正整数m满足m>3,c2,c3,cm成等差数列,
则2c3=c2+cm,
∴ ![]() =
= ![]() +
+ ![]() ,化为:2m﹣2=m.
,化为:2m﹣2=m.
m=4时,满足:2m﹣2=m.
m≥5时,2m﹣2﹣m=(1+1)m﹣2﹣m
=1+ ![]() +
+ ![]() +
+ ![]() +…﹣m
+…﹣m
=1+m﹣2+ ![]() +
+ ![]() +…﹣m
+…﹣m
= ![]() +
+ ![]() +…﹣1>0.
+…﹣1>0.
∴m≥5时,2m﹣2﹣m>0,因此2m﹣2=m无解.
综上只有m=4时,满足m>3,c2,c3,cm成等差数列
【解析】(1)(n+1)a2n+1+an+1an﹣na ![]() =0,因式分解为[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.可得
=0,因式分解为[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.可得 ![]() =
= ![]() .利用an=
.利用an= ![]()
![]() …
… ![]() a1 , 可得an . 数列{bn}的前n项和为Sn且Sn=1﹣bn . n≥2时,bn=Sn﹣Sn﹣1 , 化为:bn=
a1 , 可得an . 数列{bn}的前n项和为Sn且Sn=1﹣bn . n≥2时,bn=Sn﹣Sn﹣1 , 化为:bn= ![]() bn﹣1 . n=1时,b1=S1=1﹣b1 , 解得b1 . 利用等比数列的通项公式即可得出bn . (2)①cn=
bn﹣1 . n=1时,b1=S1=1﹣b1 , 解得b1 . 利用等比数列的通项公式即可得出bn . (2)①cn= ![]() =
= ![]() ,利用错位相减法与等比数列的求和公式即可得出.②假设存在正整数m满足m>3,c2 , c3 , cm成等差数列,2c3=c2+cm , 代入化为:2m﹣2=m.对m分类讨论即可得出.
,利用错位相减法与等比数列的求和公式即可得出.②假设存在正整数m满足m>3,c2 , c3 , cm成等差数列,2c3=c2+cm , 代入化为:2m﹣2=m.对m分类讨论即可得出.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】以下判断正确的个数是( )
①相关系数![]() 值越小,变量之间的相关性越强.
值越小,变量之间的相关性越强.
②命题“存在![]() ”的否定是“不存在
”的否定是“不存在![]() ”.
”.
③“![]() ”为真是“
”为真是“![]() ”为假的必要不充分条件.
”为假的必要不充分条件.
④若回归直线的斜率估计值是1.23,样本点的中心为(4,5),则回归直线方程是![]() .
.
A. 4 B. 2 C. 3 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)都是定义在R上的函数,且满足以下条件:
①f(x)=axg(x)(a>0,a≠1);
②g(x)≠0;
③f(x)g'(x)>f'(x)g(x);
若 ![]() ,则a= .
,则a= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占![]() ,女生中喜欢数学课程的占
,女生中喜欢数学课程的占![]() ,得到如下列联表.
,得到如下列联表.
喜欢数学课程 | 不喜欢数学课程 | 合计 | |
男生 | |||
女生 | |||
合计 |
(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;
(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,求抽取的学生中至少有1名是女生的概率..
附:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在(﹣∞,+∞)上的增函数,实数a使得f(1﹣ax﹣x2)<f(2﹣a)对于任意x∈[0,1]都成立,则实数a的取值范围是( )
A.(﹣∞,1)
B.[﹣2,0]
C.(﹣2﹣2 ![]() ,﹣2+2
,﹣2+2 ![]() )
)
D.[0,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com