
【题目】设函数f(x)=|ex﹣e2a|,若f(x)在区间(﹣1,3﹣a)内的图象上存在两点,在这两点处的切线互相垂直,则实数a的取值范围是 .
【答案】(﹣ ![]() ,
, ![]() )
)
【解析】解:当x≥2a时,f(x)=|ex﹣e2a|=ex﹣e2a , 此时为增函数,
当x<2a时,f(x)=|ex﹣e2a|=﹣ex+e2a , 此时为减函数,
即当x=2a时,函数取得最小值0,
设两个切点为M(x1 , f(x1)),N((x2 , f(x2)),
由图象知,当两个切线垂直时,必有,x1<2a<x2 ,
即﹣1<2a<3﹣a,得﹣ ![]() <a<1,
<a<1,
∵k1k2=f′(x1)f′(x2)=ex1(﹣ex2)=﹣ex1+x2=﹣1,
则ex1+x2=1,即x1+x2=0,
∵﹣1<x1<0,∴0<x2<1,且x2>2a,
∴2a<1,解得a< ![]() ,
,
综上﹣ ![]() <a<
<a< ![]() ,
,
所以答案是:(﹣ ![]() ,
, ![]() ).
).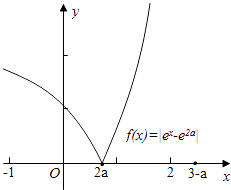


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 , (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log3a1+log3a2+…+log3an , 求数列{ ![]() }的前n项和.
}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1+x﹣2(e为自然对数的底数).g(x)=x2﹣ax﹣a+3.若存在实数x1 , x2 , 使得f(x1)=g(x2)=0.且|x1﹣x2|≤1,则实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}满足a1=1,(n+1)a2n+1+an+1an﹣na ![]() =0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
=0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
(1)求{an}和{bn}的通项;
(2)令cn= ![]() , ①求{cn}的前n项和Tn;
, ①求{cn}的前n项和Tn;
②是否存在正整数m满足m>3,c2 , c3 , cm成等差数列?若存在,请求出m;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1,﹣2)和( ![]() ,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com