
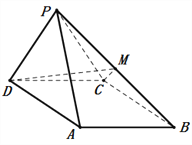
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,侧面
,侧面![]() 为等边三角形,且与底面
为等边三角形,且与底面![]() 垂直,
垂直, ![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证: ![]()
![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转 ![]() 得到半径OB.设∠POA=x(0<x<π),
得到半径OB.设∠POA=x(0<x<π), ![]() .
. 
(1)若 ![]() ,求点B的坐标;
,求点B的坐标;
(2)求函数f(x)的最小值,并求此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P在正方体ABCD﹣A1B1C1D1的面对角线BC1上运动,则下列四个结论:
①三棱锥A﹣D1PC的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面PDB1⊥平面ACD1 .
其中正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):

若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C过点A(﹣ ![]() ,1),且与x2﹣3y2=1有相同的渐近线.
,1),且与x2﹣3y2=1有相同的渐近线.
(1)求双曲线C的标准方程;
(2)过双曲线C的一个焦点作倾斜角为45°的直线l与双曲线交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
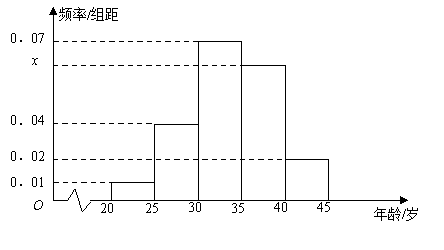
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者. 从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是: ![]() .
.
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人. 记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com