
ΓΨΧβΡΩΓΩΒΎ26Ϋλ άΫγ¥σ―ß…ζœΡΦΨ‘ΥΕ·ΜαΫΪ”Ύ2011Ρξ8‘¬12»’ΒΫ23»’‘Ύ…νέΎΨΌ–– Θ§ΈΣΝΥΗψΚΟΫ”¥ΐΙΛΉςΘ§ΉιΈ·Μα‘ΎΡ≥―ß‘Κ’–ΡΦΝΥ12ΟϊΡ–÷Ψ‘Η’ΏΚΆ18Οϊ≈°÷Ψ‘Η’ΏΓΘΫΪ’β30Οϊ÷Ψ‘Η’ΏΒΡ…μΗΏ±ύ≥…»γ”“Υυ ΨΒΡΨΞ“ΕΆΦΘ®ΒΞΈΜΘΚcmΘ©ΘΚ

»τ…μΗΏ‘Ύ175cm“‘…œΘ®Αϋά®175cmΘ©Ε®“εΈΣΓΑΗΏΗωΉ”Γ±Θ§…μΗΏ‘Ύ175cm“‘œ¬Θ®≤ΜΑϋά®175cmΘ©Ε®“εΈΣΓΑΖ«ΗΏΗωΉ”Γ±Θ§«“÷Μ”–ΓΑ≈°ΗΏΗωΉ”Γ±≤≈ΒΘ»ΈΓΑάώ“«–ΓΫψΓ±ΓΘ
Θ®1Θ©»γΙϊ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”ΓΑΗΏΗωΉ”Γ±ΚΆΓΑΖ«ΗΏΗωΉ”Γ±÷–Χα»Γ5»ΥΘ§‘Ό¥”’β5»Υ÷–―Γ2»ΥΘ§Ρ«Ο¥÷Ν…Ό”–“Μ»Υ «ΓΑΗΏΗωΉ”Γ±ΒΡΗ≈¬ «Εύ…ΌΘΩ
Θ®2Θ©»τ¥”Υυ”–ΓΑΗΏΗωΉ”Γ±÷–―Γ3Οϊ÷Ψ‘Η’ΏΘ§”Ο![]() ±μ ΨΥυ―Γ÷Ψ‘Η’Ώ÷–ΡήΒΘ»ΈΓΑάώ“«–ΓΫψΓ±ΒΡ»Υ ΐΘ§ ‘–¥≥ω
±μ ΨΥυ―Γ÷Ψ‘Η’Ώ÷–ΡήΒΘ»ΈΓΑάώ“«–ΓΫψΓ±ΒΡ»Υ ΐΘ§ ‘–¥≥ω![]() ΒΡΖ÷≤ΦΝ–Θ§≤Δ«σ
ΒΡΖ÷≤ΦΝ–Θ§≤Δ«σ![]() ΒΡ ΐ―ßΤΎΆϊΓΘ
ΒΡ ΐ―ßΤΎΆϊΓΘ
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΦϊΫβΈω.
ΘΜΘ®2Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΨΞ“ΕΆΦΘ§”–ΓΑΗΏΗωΉ”Γ±12»ΥΘ§ΓΑΖ«ΗΏΗωΉ”Γ±18»ΥΘ§”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®―Γ÷–ΒΡΓΑΗΏΗωΉ”Γ±”–2»ΥΘ§ΓΑΖ«ΗΏΗωΉ”Γ±”–3»ΥΘ°”…¥Υάϊ”ΟΕ‘ΝΔ ¬ΦΰΗ≈¬ ΦΤΥψΙΪ ΫΡή«σ≥ω÷Ν…Ό”–“Μ»Υ «ΓΑΗΏΗωΉ”Γ±ΒΡΗ≈¬ Θ°
Θ®2Θ©“άΧβ“βΘ§ΠΈΒΡ»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ°Ζ÷±π«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§”…¥ΥΡή«σ≥ωΠΈΒΡΖ÷≤ΦΝ–Θ°
‘ΧβΫβΈωΘΚ
Θ®1Θ©ΗυΨίΨΞ“ΕΆΦΘ§”–ΓΑΗΏΗωΉ”Γ±12»ΥΘ§ΓΑΖ«ΗΏΗωΉ”Γ±18»ΥΘ§
”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®Θ§ΟΩΗω»Υ±Μ≥ι÷–ΒΡΗ≈¬ «![]() Θ§
Θ§
Υυ“‘―Γ÷–ΒΡΓΑΗΏΗωΉ”Γ±”–![]() »ΥΘ§ΓΑΖ«ΗΏΗωΉ”Γ±”–
»ΥΘ§ΓΑΖ«ΗΏΗωΉ”Γ±”–![]() »ΥΘ°
»ΥΘ°
”Ο ¬Φΰ![]() ±μ ΨΓΑ÷Ν…Ό”–“ΜΟϊΓΑΗΏΗωΉ”Γ±±Μ―Γ÷–Γ±Θ§‘ρΥϋΒΡΕ‘ΝΔ ¬Φΰ
±μ ΨΓΑ÷Ν…Ό”–“ΜΟϊΓΑΗΏΗωΉ”Γ±±Μ―Γ÷–Γ±Θ§‘ρΥϋΒΡΕ‘ΝΔ ¬Φΰ![]() ±μ ΨΓΑΟΜ”–“ΜΟϊΓΑΗΏΗωΉ”Γ±±Μ―Γ÷–Γ±Θ§
±μ ΨΓΑΟΜ”–“ΜΟϊΓΑΗΏΗωΉ”Γ±±Μ―Γ÷–Γ±Θ§
ΓΓ‘ρ Θ°
Θ°
“ρ¥ΥΘ§÷Ν…Ό”–“Μ»Υ «ΓΑΗΏΗωΉ”Γ±ΒΡΗ≈¬ «![]() Θ°
Θ°
Θ®Θ≤Θ©“άΧβ“βΘ§ ![]() ΒΡ»Γ÷ΒΈΣ
ΒΡ»Γ÷ΒΈΣ![]() Θ°
Θ°
ΓΓ Θ§ΓΓΓΓΓΓ
Θ§ΓΓΓΓΓΓ Θ§
Θ§
ΓΓ Θ§
Θ§  Θ°
Θ°
ΓΓ“ρ¥ΥΘ§ ![]() ΒΡΖ÷≤ΦΝ–»γœ¬ΘΚ
ΒΡΖ÷≤ΦΝ–»γœ¬ΘΚ
|
|
|
|
|
|
|
|
|
|
![]() Θ°
Θ°


 ΩΎΥψΧβΩ®Φ””Π”ΟΧβΦ·―ΒœΒΝ–¥πΑΗ
ΩΎΥψΧβΩ®Φ””Π”ΟΧβΦ·―ΒœΒΝ–¥πΑΗ ΉέΚœΉ‘≤βœΒΝ–¥πΑΗ
ΉέΚœΉ‘≤βœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψΘ®1Θ§©¹2Θ©ΚΆΘ® ![]() Θ§0Θ©‘Ύ÷±œΏlΘΚax©¹y©¹1=0Θ®aΓΌ0Θ©ΒΡΝΫ≤ύΘ§‘ρ÷±œΏlΒΡ«ψ–±Ϋ«ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
Θ§0Θ©‘Ύ÷±œΏlΘΚax©¹y©¹1=0Θ®aΓΌ0Θ©ΒΡΝΫ≤ύΘ§‘ρ÷±œΏlΒΡ«ψ–±Ϋ«ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
A.Θ® ![]() Θ§
Θ§ ![]() Θ©
Θ©
B.Θ® ![]() Θ§
Θ§ ![]() Θ©
Θ©
C.Θ® ![]() Θ§
Θ§ ![]() Θ©
Θ©
D.Θ®0Θ§ ![]() Θ©Γ»Θ®
Θ©Γ»Θ® ![]() Θ§Π–Θ©
Θ§Π–Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ,
, ![]()
(1)Β±a=1 ±Θ§«σ«ζœΏ ΐ![]() ‘ΎΒψ(1Θ§
‘ΎΒψ(1Θ§ ![]() )¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
)¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
(2)»τ![]() ±Θ§Κ· ΐ ΐ
±Θ§Κ· ΐ ΐ![]() ΒΡΉν–Γ÷ΒΈΣ0Θ§«σaΒΡ»Γ÷ΒΖΕΈßΓΘ
ΒΡΉν–Γ÷ΒΈΣ0Θ§«σaΒΡ»Γ÷ΒΖΕΈßΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() «±Ώ≥ΛΈΣ
«±Ώ≥ΛΈΣ![]() ΒΡΝβ–ΈΘ§«“
ΒΡΝβ–ΈΘ§«“![]() Θ§≤ύΟφ
Θ§≤ύΟφ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§«“”κΒΉΟφ
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§«“”κΒΉΟφ![]() ¥Ι÷±Θ§
¥Ι÷±Θ§ ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
Θ®ΔώΘ©«σ÷ΛΘΚ ![]()
![]() ΘΜ
ΘΜ
Θ®ΔρΘ©«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
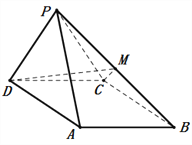
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐ![]() Θ§
Θ§ ![]() Θ°
Θ°
Θ®ΔώΘ©«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®ΔρΘ©Β±![]() ±Θ§Χ÷¬έΚ· ΐ
±Θ§Χ÷¬έΚ· ΐ![]() ”κ
”κ![]() ΆΦœώΒΡΫΜΒψΗω ΐΘ°
ΆΦœώΒΡΫΜΒψΗω ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an}ΒΡ«ΑnœνΚΆΈΣSn Θ§ «“¬ζΉψSn=n2©¹4nΘ§ ΐΝ–{bn}÷–Θ§b1= ![]() Ε‘»Έ“β’ΐ’ϊ ΐ
Ε‘»Έ“β’ΐ’ϊ ΐ ![]() Θ°
Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐΠΧΘ§ ΙΒΟ ΐΝ–{3nbn+ΠΧ} «Β»±» ΐΝ–ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω Β ΐΠΧΦΑΙΪ±»qΒΡ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©«σ÷ΛΘΚ ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗω―υ±ΨMΒΡ ΐΨί «x1 Θ§ x2 Θ§ Γ≠Θ§xn Θ§ ΥϋΒΡΤΫΨυ ΐ «5Θ§Νμ“ΜΗω―υ±ΨNΒΡ ΐΨίx12 Θ§ x22 Θ§ Γ≠Θ§xn2ΥϋΒΡΤΫΨυ ΐ «34Θ°Ρ«Ο¥œ¬ΟφΒΡΫαΙϊ“ΜΕ®’ΐ»ΖΒΡ «Θ® Θ©
A.SM2=9
B.SN2=9
C.SM2=3
D.Sn2=3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ{an} «“ΜΗωΒ»≤ν ΐΝ–«“a2+a8=©¹4Θ§a6=2
Θ®1Θ©«σ{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©«σ{an}ΒΡ«ΑnœνΚΆSnΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ»ΐάβΉΕ![]() ÷–Θ§
÷–Θ§ ![]() ΓΆΤΫΟφ
ΓΆΤΫΟφ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΒΡ÷–ΒψΘ°(19)
ΒΡ÷–ΒψΘ°(19)
(I)«σ![]() ΒΫΤΫΟφ
ΒΫΤΫΟφ![]() ΒΡΨύάκΘΜ
ΒΡΨύάκΘΜ
(II)‘ΎœΏΕΈ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψ
…œ «Ζώ¥φ‘Ύ“ΜΒψ![]() Θ§ ΙΒΟΤΫΟφ
Θ§ ΙΒΟΤΫΟφ![]() ΓΈΤΫΟφ
ΓΈΤΫΟφ![]() Θ§»τ¥φ‘ΎΘ§ ‘»ΖΕ®
Θ§»τ¥φ‘ΎΘ§ ‘»ΖΕ®![]() ΒΡΈΜ÷ΟΘ§≤Δ÷ΛΟς¥ΥΒψ¬ζΉψ“Σ«σΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΈΜ÷ΟΘ§≤Δ÷ΛΟς¥ΥΒψ¬ζΉψ“Σ«σΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
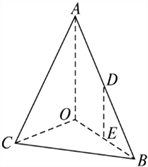
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com