
分析 (1)利用导数直接求单调区间;
(2)若要命题成立,只需当x∈(0,2]时,f(x)max<g(x)max.分别求出最大值即可.
解答 解:(1)f′(x)=ax-(2a+1)+$\frac{2}{x}$,…(2分)
所以a=$\frac{2}{3}$时,f′(x)=$\frac{(2x-3)(x-2)}{3x}$,
其单调递增区间为(0,$\frac{3}{2}$),(2,+∞),单调递减区间为($\frac{3}{2},2))$. …(5分)
(2)若要命题成立,只需当x∈(0,2]时,f(x)max<g(x)max.
由g′(x)=(x2-2)ex可知,当x∈(0,2]时,g(x)在区间(0,$\sqrt{2}$)上单调递减,在区间($\sqrt{2}$,2]上单调递增,
g(0)=g(2)=0,故g(x)max=0,…(7分)
所以只需f(x)max<0.
对函数f(x)来说,f′(x)=ax-(2a+1)+$\frac{2}{x}$=$\frac{(ax-1)(x-2)}{x}$
当a≤0时,由x∈(0,2],f′(x)≥0,函数f(x)在区间(0,2]上单调递增,
f(x)max=f(2)=2ln2-2a-2<0,故ln2-1<a≤0
当0<a≤2时,$\frac{1}{a}≥2$,由x∈(0,2),ax-1≥0,故f′(x)≥0,
函数f(x)在区间(0,2)上单调递增,
f(x)max=f(2)=2ln2-2a-2<0,a>ln2-1
故0<a≤2满足题意
当a>$\frac{1}{2}$时,$0<\frac{1}{a}<2$,函数f(x)在区间(0,$\frac{1}{a}$)上单调递增,在区间($\frac{1}{a},2)$上单调递减,
f(x)max=f($\frac{1}{a})$=-2lna-$\frac{1}{2a}$-2.
若a≥1时,显然小于0,满足题意;
若$\frac{1}{2}<a<1$时,可令h(a)=-2lna-$\frac{1}{2a}$-2,$h′(a)=\frac{1-4a}{2{a}^{2}}$,
可知该函数在$\frac{1}{2}<a<1$时单调递减,
$h(a)<h(\frac{1}{2})=2ln2-3<0$,满足题意,所以a>$\frac{1}{2}$满足题意.
综上所述:实数a的取值范围是(ln2-1,+∞) …(14分)
点评 本题考查了函数的单调性及存在、任意的处理方法,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
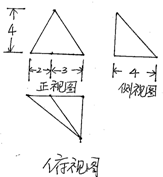
| A. | $\frac{80}{\begin{array}{l}3\end{array}}$ | B. | $\frac{40}{\begin{array}{l}3\end{array}}$ | C. | 80 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com