
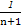 +
+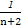 +…+
+…+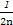 >
>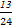 (n∈N*且n>1).
(n∈N*且n>1). 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
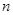 个图包含______个互不重叠的单位正方形。
个图包含______个互不重叠的单位正方形。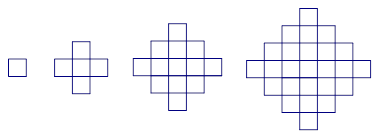
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1 |
| B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k |
C.式子1+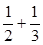 +…+ +…+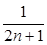 (n∈N*)中,当n=1时式子值为1+ (n∈N*)中,当n=1时式子值为1+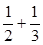 |
D.设f(x)=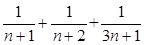 (n∈N*),则f(k+1)=f(k)+ (n∈N*),则f(k+1)=f(k)+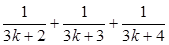 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.18 | B.36 | C.48 | D.54 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
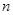 条两两相交的弦,把圆最多分成 部分.
条两两相交的弦,把圆最多分成 部分.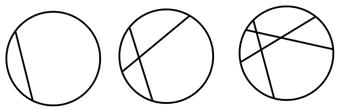
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
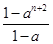 (n∈N*,a≠1),在验证n=1时,左边所得的项为( )
(n∈N*,a≠1),在验证n=1时,左边所得的项为( )| A.1 | B.1+a+a2 | C.1+a | D.1+a+a2+a3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com