
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,设函数
时,设函数![]() 有最小值
有最小值![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)见解析;(2) 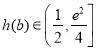
【解析】
(1)先求出![]() ,分
,分![]() 和
和![]() 两种情形,利用导数的符号判断函数的单调性即可.
两种情形,利用导数的符号判断函数的单调性即可.
(2)求出![]() 并将其化简为
并将其化简为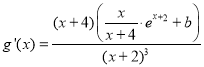 ,构建新函数
,构建新函数![]() ,利用(1)的单调性及零点存在定理可得
,利用(1)的单调性及零点存在定理可得![]() 有唯一的
有唯一的![]() ,它就是函数
,它就是函数![]() 最小值点,利用导数可求该最小值的值域.
最小值点,利用导数可求该最小值的值域.
解:(1)![]() 定义域为
定义域为![]() ,
,
![]()
![]() .
.
令![]() ,①
,①
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,
即![]() 且不恒为零,故
且不恒为零,故![]() 单调递增区间为
单调递增区间为![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,方程①两根为
,方程①两根为![]() ,
,![]() ,
,
由于![]() ,
,
![]() .
.
故![]() ,
,
因此当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
综上,当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,![]() 单调递减;
单调递减;
在![]() 单调递增.
单调递增.
(2)![]()
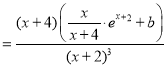 ,
,
设![]() ,
,
由(1)知,![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
由于![]() ,
,![]() ,
,
故在![]() 存在唯一
存在唯一![]() ,使
,使![]() ,
,
![]() ,
,
又当![]() ,
,![]() ,即
,即![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,![]() ,即
,即![]() ,
,![]() 单调递增,
单调递增,
故![]() 时,
时,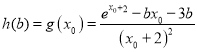
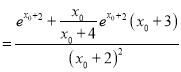
![]() ,
,![]() .
.
又设![]() ,
,![]() ,
,
![]() ,
,
故![]() 单调递增,故
单调递增,故![]() ,
,
即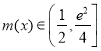 ,即
,即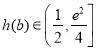 .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,且
,且![]() 在底
在底![]() 内的射影恰为
内的射影恰为![]() 的中点
的中点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点.
上任意一点.
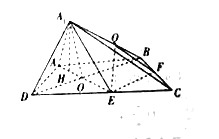
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 经过椭圆C的上、下顶点.
经过椭圆C的上、下顶点.
(1)求椭圆C的方程;
(2)若直线l与椭圆C相切,且与椭圆![]() 相交于M,N两点,证明:
相交于M,N两点,证明:![]() 的面积为定值(O为坐标原点).
的面积为定值(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 另一个焦点是
另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的内切圆面积的最大值.
的内切圆面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为5.
的距离为5.
(1)求![]() 与
与![]() 的值;
的值;
(2)设动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在与
轴上是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
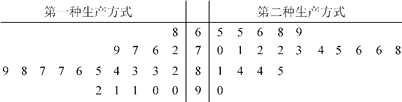
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com