
设f(x)=- x3+
x3+ x2+2ax.
x2+2ax.
(1)若f(x)在( ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为-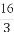 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
(1) a>-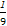 (2) f(x)max=
(2) f(x)max=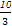
【解析】(1)f(x)=-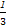 x3+
x3+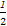 x2+2ax,
x2+2ax,
∴f'(x)=-x2+x+2a,当x∈[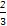 ,+∞)时,f'(x)的最大值为f'(
,+∞)时,f'(x)的最大值为f'(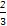 )=
)=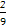 +2a.
+2a.
函数f(x)在(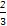 ,+∞)上存在单调递增区间,即导函数在(
,+∞)上存在单调递增区间,即导函数在(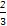 ,+∞)上存在函数值大于零成立,
,+∞)上存在函数值大于零成立,
∴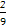 +2a>0
+2a>0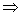 a>-
a>-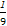 .
.
(2)已知0<a<2,f(x)在[1,4]上取到最小值-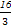 ,而f'(x)=-x2+x+2a的图象开口向下,且对称轴为x=
,而f'(x)=-x2+x+2a的图象开口向下,且对称轴为x=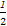 ,
,
∴f'(1)=-1+1+2a=2a>0,
f'(4)=-16+4+2a=2a-12<0,
则必有一点x0∈[1,4]使得f'(x0)=0,此时函数f(x)在[1,x0]上单调递增,在[x0,4]上单调递减,
f(1)=-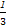 +
+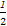 +2a=
+2a=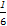 +2a>0,
+2a>0,
∴f(4)=-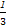 ×64+
×64+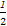 ×16+8a=-
×16+8a=-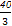 +8a,
+8a,
∴-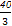 +8a=-
+8a=-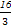 ,得a=1,
,得a=1,
此时,由f'(x0)=-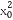 +x0+2=0得x0=2或-1(舍去),
+x0+2=0得x0=2或-1(舍去),
所以函数f(x)max=f(2)=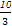 .
.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:填空题
将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D -ABC的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
某个命题与正整数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立,现已知n=5时,该命题不成立,那么可以推得
(A)n=6时该命题不成立 (B)n=6时该命题成立
(C)n=4时该命题不成立 (D)n=4时该命题成立
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
已知函数f(x)=( )x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:
)x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为 .(将你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:填空题
若函数f(x)=x(x-c)2在x=2处有极大值,则常数c的值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:选择题
设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则( )
(A)a<-1 (B)a>-1
(C)a>- (D)a<-
(D)a<-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:解答题
已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求cos3(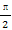 -θ)+sin3(
-θ)+sin3(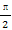 -θ)的值.
-θ)的值.
(2)求tan(π-θ)-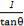 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:选择题
某厂日产手套总成本y(元)与手套日产量x(副)的关系式为y=5x+4000,而手套出厂价格为每副10元,则该厂为了不亏本,日产手套至少为( )
(A)200副 (B)400副 (C)600副 (D)800副
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com