
某个命题与正整数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立,现已知n=5时,该命题不成立,那么可以推得
(A)n=6时该命题不成立 (B)n=6时该命题成立
(C)n=4时该命题不成立 (D)n=4时该命题成立
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:填空题
棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,若棱AA1,DD1的中点分别为E,F,则直线EF被球O截得的弦长为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:填空题
已知点A(1,2,1),B(-1,3,4),D(1,1,1),若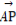 =2
=2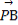 ,则|
,则|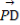 |的值是______.
|的值是______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:解答题
设函数f(x)满足2f(x)-f(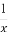 )=4x-
)=4x- +1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
(1)求f(x)的解析式.
(2)求{bn}的通项公式bn.
(3)试比较2an与bn的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,f(n)都能被m整除,则m的最大值为( )
(A)18 (B)36 (C)48 (D)54
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:解答题
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
若P=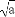 +
+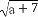 ,Q=
,Q=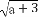 +
+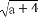 (a≥0),则P,Q的大小关系是( )
(a≥0),则P,Q的大小关系是( )
(A)P>Q (B)P=Q
(C)P<Q (D)由a的取值确定
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:解答题
设f(x)=- x3+
x3+ x2+2ax.
x2+2ax.
(1)若f(x)在( ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为-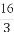 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:选择题
已知α∈(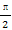 ,π),tanα=-
,π),tanα=- ,则sin(α+π)=( )
,则sin(α+π)=( )
(A) (B)-
(B)- (C)
(C) (D)-
(D)-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com