
当![]() 为正整数时,区间
为正整数时,区间![]() ,
,![]() 表示函数
表示函数![]() 在
在![]() 上函数值取整数值的个数,当
上函数值取整数值的个数,当![]() 时,记
时,记![]() .当
.当![]() ,
,![]() 表示把
表示把![]() “四舍五入”到个位的近似值,如
“四舍五入”到个位的近似值,如![]()
![]() 当
当![]() 为正整数时,
为正整数时,![]() 表示满足
表示满足![]() 的正整数
的正整数![]() 的个数.
的个数.
(1)判断![]() 在区间
在区间![]() 的单调性;
的单调性;
(2)求![]() ;
;
(3)当![]() 为正整数时,集合
为正整数时,集合![]() 中所有元素之和为
中所有元素之和为![]() ,记
,记![]() 求证:
求证:![]()
(1)当![]()
![]()
![]() 为增函数(2)
为增函数(2)![]()
![]()
![]()
![]() (3)见解析
(3)见解析
(1)∵![]()
∴当![]()
![]()
![]() 为增函数.----------------------2分
为增函数.----------------------2分
(2)由(1) ![]() 在
在![]() 为增函数,又
为增函数,又![]()
∴![]() --------------------------------------------------3分
--------------------------------------------------3分
同理![]() 时,
时,![]()
![]() 为增函数,
为增函数,
![]() ∴
∴![]() -----------------------4分
-----------------------4分
∴![]() -----------------------------------------5分
-----------------------------------------5分
又∵![]() 表示满足
表示满足![]() 的正整数
的正整数![]() 的个数.
的个数.
∴![]()
∴![]()
![]()
∴![]() -----------------------------------------------6分
-----------------------------------------------6分
(3)又∵![]() 表示满足
表示满足![]() 的正整数
的正整数![]() 的个数,
的个数,
∴![]() --------------------------------8分
--------------------------------8分
∴![]()
∴![]() 共
共![]() 个.
个.
∴![]() ------------------------------------------10分
------------------------------------------10分
![]()
![]()
∴![]()
![]()
![]()
![]()
![]()
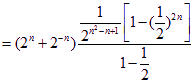 =
=![]()
![]() ----------------------------------------12分
----------------------------------------12分
∴![]()
![]()
![]()
![]() ----------------14分
----------------14分


科目:高中数学 来源: 题型:
| x(x-1)…(x-m+1) |
| m! |
| ||
|
查看答案和解析>>
科目:高中数学 来源:2008年高考冲刺解答题突破、数学 题型:044
当n为正整数时,区间In=(n,n+1),an表示函数![]() 在In上函数值取整数值的个数,当n>1时,记bn=an-an-1.当x>0,g(x)表示把x“四舍五入”到个位的近似值,如
在In上函数值取整数值的个数,当n>1时,记bn=an-an-1.当x>0,g(x)表示把x“四舍五入”到个位的近似值,如![]()
![]() 当n为正整数时,cn表示满足
当n为正整数时,cn表示满足![]() 的正整数k的个数.
的正整数k的个数.
(Ⅰ)求b2,c2;
(Ⅱ)求证:n>1时,bn=cn;
(Ⅲ)当n为正整数时,集合![]() 中所有元素之和为Sn,记Tn=(2n+2-n)Sn,求证:T1+T2+T3+…Tn<3.
中所有元素之和为Sn,记Tn=(2n+2-n)Sn,求证:T1+T2+T3+…Tn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() (
(![]() >0),过点P(1,0)作曲线
>0),过点P(1,0)作曲线![]() 的两条切线PM、PN,为M、N.
的两条切线PM、PN,为M、N.
(1)当t=2时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设|MN|=g(t),求函数g(t)的表达式;
(3)在(2)的条件下,若对任意正整数![]() ,在区间[2,
,在区间[2,![]() +
+![]() ]内总存在
]内总存在![]() +1个实数
+1个实数![]() 、
、![]() 、…、
、…、![]() 、
、![]() ,使得不等式g(
,使得不等式g(![]() )+g(
)+g(![]() )+…+g(
)+…+g(![]() )<g(
)<g(![]() )成立,求
)成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2011年云南省高三数学一轮复习章节练习:计数原理(解析版) 题型:解答题
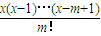 ,其中x∈R,m是正整数,且Cx=1,这是组合数Cmn(n、m是正整数,且m≤n)的一种推广.
,其中x∈R,m是正整数,且Cx=1,这是组合数Cmn(n、m是正整数,且m≤n)的一种推广.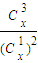 取得最小值?
取得最小值?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com