Question

13．若△ABC的外接圆圆心O，垂心是H，求证：$\overrightarrow{OH}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$．

Answer 1

分析 作出如图的图形，可证得四边形AHBE是平行四边形，从研究$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$入手，利用三角形法则与图象进行整理，将三者的和用$\overrightarrow{OH}$表示出来可得结论．

解答 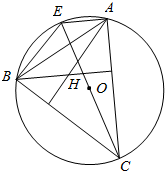证明：∵△ABC的外接圆圆心O，垂心是H，
∴H是BC边与AC边上高的交点．
连接CO并延长交圆O于E，连接AE，BE．
由CE是圆的直径可知∠CAE=∠CBE=90°，
即EA垂直AC，EB垂直BC．
∵H是两边高上的交点，即AH垂直BC，BH垂直AC，
∴有AH平行BE，BH平行AE，
∴四边形BEAH是平行四边形，
从而向量$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{EO}$=$\overrightarrow{OA}$+$\overrightarrow{EB}$=$\overrightarrow{OA}$+$\overrightarrow{AH}$=$\overrightarrow{OH}$，
即向量$\overrightarrow{OH}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$．

点评 本题考查三角形的五心，解答本题，关键是根据题意，构造出平行四边形，再利用向量运算，将三个向量的和表示出来，本题中选择入手的位置很关键，此类似于代数中的化简式证明．作题时注意构造法思想的运用，向量在几何中的运用．