Question

2．如图，在长方体ABCD-A₁B₁C₁D₁中，E是矩形BCC₁B₁的中点，F是矩形ADD₁A₁的中心，连接AE，B₁F，判断AE与B₁F是否为异面直线．

Answer 1

分析 取B₁C₁的中点G，AA₁的中点H，证明AE∥HG，B₁，G，F，H在同一平面内，利用AE与平面B₁GFH无公共点，而B₁F在此平面上，故AE与B₁F也无公共点，可得结论．

解答 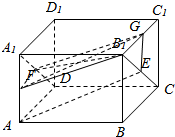解：取B₁C₁的中点G，AA₁的中点H．连接EG，GH，知EG∥BB1₁∥AA₁，且EG=AH，故AEGH为平行四边形．
从而知：AE∥HG．
连接HF，HB₁，FG．知B₁G∥HF，即知B₁，G，F，H在同一平面内．
∴AE平行于平面B₁GFH，
由于AE∥HG，而HG与B₁F相交，故AE不平行于B₁F．
又：AE与平面B₁GFH无公共点，而B₁F在此平面上，故AE与B₁F也无公共点．
从而知AE，B₁F为异面直线．

点评 本题考查线面平行、异面直线的证明，考查学生分析解决问题的能力，属于中档题．