
分析 (1)求出函数y=x+e-x的导数,求得单调区间,可得最小值,再由不等式的性质,即可得证;
(2)由题意可得a>$\frac{x+{e}^{-x}-1}{{x}^{2}}$的最大值,构造g(x)=$\frac{x+{e}^{-x}-1}{{x}^{2}}$-$\frac{1}{2}$,只需证得g(x)≤0在x>0恒成立,即为x+e-x-1-$\frac{1}{2}$x2≤0,由h(x)=x+e-x-1-$\frac{1}{2}$x2的导数为1-e-x-x,再由ex≥x+1,即可得到a的范围.
解答 解:(1)证明:函数y=x+e-x的导数为y′=1-e-x,
当x>0时,函数y′>0,函数递增;
当x<0时,函数y′<0,函数递减.
即有x=0处取得最小值,且为1,
即y≥1,由“置换函数”的定义可得f(x)∈(0,1];
(2)由在x∈(0,+∞)区间上(ax2+1)f(x)>1成立,
即为a>$\frac{x+{e}^{-x}-1}{{x}^{2}}$的最大值,
构造g(x)=$\frac{x+{e}^{-x}-1}{{x}^{2}}$-$\frac{1}{2}$,只需证得g(x)≤0在x>0恒成立,
即为x+e-x-1-$\frac{1}{2}$x2≤0,
由h(x)=x+e-x-1-$\frac{1}{2}$x2的导数为1-e-x-x,
由ex-x-1的导数为ex-1,可得x>0,函数递增;x<0,函数递减.
即有x=0处取得最小值0,即有ex≥x+1,
即有e-x≥-x+1,即为1-e-x-x≤0,
可得h(x)在x>0递减,即有h(x)<h(0)=0,
则g(x)≤0在x>0恒成立,
即有a>$\frac{1}{2}$.
点评 本题考查新定义的理解和运用,考查导数的运用:求单调区间和最值,考查不等式恒成立问题的解法,注意运用参数分离,构造函数运用导数求最值,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
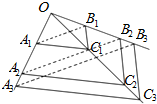 如图,互不相同的点A1、A2、…An、…,B1、B2、…Bn、…,C1、C2、…、Cn、…分别在以O为顶顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\root{3}{2}$,a2=2,则an=$\root{3}{6n-4}$.
如图,互不相同的点A1、A2、…An、…,B1、B2、…Bn、…,C1、C2、…、Cn、…分别在以O为顶顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\root{3}{2}$,a2=2,则an=$\root{3}{6n-4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (3,+∞) | C. | [2,3] | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | D. | -$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com