
 桑基鱼塘是某地一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块1800平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为2米,如图,设池塘所占总面积为S平方米.
桑基鱼塘是某地一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块1800平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为2米,如图,设池塘所占总面积为S平方米.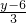
 y=1832-6x-
y=1832-6x-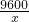 (x>0).
(x>0).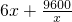 ≥
≥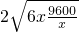 =480,当且仅当
=480,当且仅当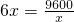 ,即x=40m时,取等号,
,即x=40m时,取等号,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com