
分析 由¬q与p∧q均为假命题,可得q为真命题,p为假命题.分别求出两个命题对应的参数的范围,进而可得答案.
解答 解:若命题p为真,则有$cos<\overrightarrow{AB},\overrightarrow{AC}>≥$0,
即$\overrightarrow{AB}•\overrightarrow{AC}=-1+{m^2}≥0$,解得m≤-1或m≥1,
若命题q为真,则有1<$\frac{5+m}{5}$<4,
解得:0<m<15,
∵¬q与p∧q均为假命题,
∴q为真命题,p为假命题.
则有$\left\{\begin{array}{l}-1<m<1\\ 0<m<15\end{array}\right.$解得0<m<1.
故所求实数m的取值范围是0<m<1.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,向量夹角,双曲线的性质等知识点,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
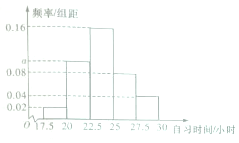 某高校调查了20名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30).
某高校调查了20名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26,21,20 | B. | 26,22,20 | C. | 30,26,20 | D. | 30,22,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{80}{883}$ | C. | $\frac{1}{12}$ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com