
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() ,
,![]() 在
在![]() 上,且
上,且![]() .
.
(1)求![]() 的值;
的值;
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 交于
交于![]() ,
,![]() (异于
(异于![]() )两点,证明:直线
)两点,证明:直线![]() 与直线
与直线![]() 的斜率之积为常数.
的斜率之积为常数.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
, ![]() ,
, ![]() ,若
,若![]() 为
为![]() 的中点,且
的中点,且![]() .
.
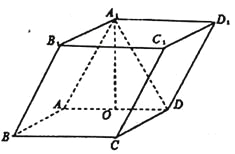
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线![]() 、
、![]() 相互垂直,与曲线C分别相交于A、B两点(不同于点O),且
相互垂直,与曲线C分别相交于A、B两点(不同于点O),且![]() 的倾斜角为锐角
的倾斜角为锐角![]() .
.
(1)求曲线C和射线![]() 的极坐标方程;
的极坐标方程;
(2)求△OAB的面积的最小值,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神舟十号”宇宙飞船进行新产品搭载实验,计划搭载新产品甲,乙,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品甲(件) | 产品乙(件) | ||
研制成本与搭载费用之和(万元/件) | 200 | 300 | 计划最大资金额3000元 |
产品重量(千克/件) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元/件) | 160 | 120 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且与
且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 和圆
和圆![]() 截得的弦长分别为2和
截得的弦长分别为2和![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 与抛物线
与抛物线![]() :
:![]() 相切(切点异于原点),且
相切(切点异于原点),且![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问:椭圆
两点,问:椭圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在求出满足条件的所有
,若存在求出满足条件的所有![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由.
参考公式与临界值表:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() ;
;
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件,为了估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量,![]() 与月份
与月份![]() 的关系,模拟函数可以选用二次函数或函数
的关系,模拟函数可以选用二次函数或函数![]() 、
、![]() 、
、![]() 为常数)已知四月份该产品的产量为1.37万件,请问用以上哪个函数作模拟函数较好?说明理由.
为常数)已知四月份该产品的产量为1.37万件,请问用以上哪个函数作模拟函数较好?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地需要修建一条大型输油管道通过720千米宽的荒漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为108万元,铺设距离为![]() 千米的相邻两增压站之间的输油管道费用为
千米的相邻两增压站之间的输油管道费用为![]() 万元.设余下工程的总费用为
万元.设余下工程的总费用为![]() 万元.
万元.
(1)试将![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(2)需要修建多少个增压站才能使总费用![]() 最小?
最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com