
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且与
且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 和圆
和圆![]() 截得的弦长分别为2和
截得的弦长分别为2和![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 与抛物线
与抛物线![]() :
:![]() 相切(切点异于原点),且
相切(切点异于原点),且![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问:椭圆
两点,问:椭圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在求出满足条件的所有
,若存在求出满足条件的所有![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,正三角形PAC所在平面与等腰三角形ABC所在平面互相垂直,AB=BC,O是AC中点,OH⊥PC于H.
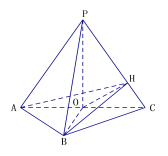
(1)证明:PC⊥平面BOH;
(2)若![]() ,求二面角A-BH-O的余弦值.
,求二面角A-BH-O的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,椭圆
的一个焦点重合,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,记直线
上一点,记直线![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() 和
和![]() ,且满足
,且满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,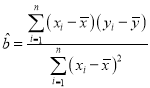
参考数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com