练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某工厂生产某种型号的农机具零配件，为了预测今年7月份该型号农机具零配件的市场需求量，以合理安排生产，工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查，销售单价（单位：元）和销售量（单位：千件）之间的6组数据如下表所示：

    月份

    1

    2

    3

    4

    5

    6

    销售单价（元）

    11.1

    9.1

    9.4

    10.2

    8.8

    11.4

    销售量（千件）

    2.5

    3.1

    3

    2.8

    3.2

    2.4

    （1）根据1至6月份的数据，求关于的线性回归方程（系数精确到0.01）；

    （2）结合（1）中的线性回归方程，假设该型号农机具零配件的生产成本为每件3元，那么工厂如何制定7月份的销售单价，才能使该月利润达到最大？（计算结果精确到0.1）

    参考公式：回归直线方程，

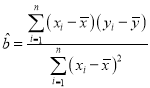
    参考数据：，

    【答案】（1）；（2）销售单价为11.3元时，该月利润才能达到最大

    【解析】

    （1）求出的平均数，利用最小二乘法即可得出关于的线性回归方程；

    （2）由题意得出7月份的利润的关系式，结合二次函数的性质，即可得出结论.

    （1）由条件知，，

    所以，

    故关于的线性回归方程为.

    （2）假设7月份的销售单价为元

    则由（1）可知，7月份零配件销量为

    故7月份的利润，

    其对称轴，故7月份销售单价为11.3元时，该月利润才能达到最大.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的左、右焦点分别为，，过且与轴垂直的直线被椭圆和圆截得的弦长分别为2和.

    （1）求的标准方程；

    （2）已知动直线与抛物线：相切（切点异于原点），且与椭圆相交于，两点，问：椭圆上是否存在点，使得，若存在求出满足条件的所有点的坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[2019·清远期末]一只红铃虫的产卵数和温度有关，现收集了4组观测数据列于下表中，根据数据作出散点图如下：

    温度

    20

    25

    30

    35

    产卵数/个

    5

    20

    100

    325

    （1）根据散点图判断与哪一个更适宜作为产卵数关于温度的回归方程类型？（给出判断即可，不必说明理由）

    （2）根据（1）的判断结果及表中数据，建立关于的回归方程（数字保留2位小数）；

    （3）要使得产卵数不超过50，则温度控制在多少以下？（最后结果保留到整数）

    参考数据：，，，，，，，，，，

    5

    20

    100

    325

    1.61

    3

    4.61

    5.78

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于空间向量的命题中，正确的有______.

    ①若向量，与空间任意向量都不能构成基底，则；

    ②若非零向量，，满足，，则有；

    ③若，，是空间的一组基底，且，则，，，四点共面；

    ④若向量，，，是空间一组基底，则，，也是空间的一组基底.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知、是椭圆和双曲线的公共焦点，是他们的一个公共点，且，则椭圆和双曲线的离心率的倒数之和的最大值为___.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地需要修建一条大型输油管道通过720千米宽的荒漠地带，该段输油管道两端的输油站已建好，余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站（又称泵站）.经预算，修建一个增压站的工程费用为108万元，铺设距离为千米的相邻两增压站之间的输油管道费用为万元.设余下工程的总费用为万元.

    （1）试将表示成关于的函数；

    （2）需要修建多少个增压站才能使总费用最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥的底面是边长为的菱形，，点是棱的中点，，点在平面的射影为，为棱上一点，

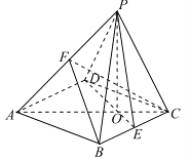
    （Ⅰ）求证：平面平面；

    （Ⅱ）若为棱的中点，，求直线与平面所成角的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2＋ax＋b，g(x)＝ex(cx＋d)，若曲线y＝f(x)和曲线y＝g(x)都过点P(0，2)，且在点P处有相同的切线y＝4x＋2．

    (1)求a，b，c，d的值；

    (2)若x≥－2时，恒有f(x)≤kg(x)，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间，需求量为300瓶；如果最高气温低于20，需求量为200瓶.为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

    以最高气温位于各区间的频率代替最高气温位于该区间的概率.

    （1）求六月份这种酸奶一天的需求量(单位:瓶)的分布列；

    （2）设六月份一天销售这种酸奶的利润为(单位:元)，当六月份这种酸奶一天的进货量（单位：瓶）为多少时？的数学期望达到最大值？

    查看答案和解析>>

    同步练习册答案