
【题目】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() ;
;
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选手接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,正确的题号是__________.
①函数的最值一定是极值;
②设![]() :实数
:实数![]() ,
,![]() 满足
满足![]() ;
;![]() :实数
:实数![]() ,
,![]() 满足
满足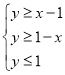 ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③已知椭圆![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的离心率,则
的离心率,则![]() ,且
,且![]() ;
;
④一动圆![]() 过定点
过定点![]() ,且与已知圆
,且与已知圆![]() :
:![]() 相切,则动圆圆心
相切,则动圆圆心![]() 的轨迹方程是
的轨迹方程是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,椭圆
的一个焦点重合,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,记直线
上一点,记直线![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() 和
和![]() ,且满足
,且满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: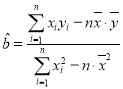 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com