
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: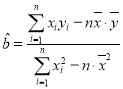 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线![]() 、
、![]() 相互垂直,与曲线C分别相交于A、B两点(不同于点O),且
相互垂直,与曲线C分别相交于A、B两点(不同于点O),且![]() 的倾斜角为锐角
的倾斜角为锐角![]() .
.
(1)求曲线C和射线![]() 的极坐标方程;
的极坐标方程;
(2)求△OAB的面积的最小值,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() ;
;
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件,为了估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量,![]() 与月份
与月份![]() 的关系,模拟函数可以选用二次函数或函数
的关系,模拟函数可以选用二次函数或函数![]() 、
、![]() 、
、![]() 为常数)已知四月份该产品的产量为1.37万件,请问用以上哪个函数作模拟函数较好?说明理由.
为常数)已知四月份该产品的产量为1.37万件,请问用以上哪个函数作模拟函数较好?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于空间向量的命题中,正确的有______.
①若向量![]() ,
,![]() 与空间任意向量都不能构成基底,则
与空间任意向量都不能构成基底,则![]() ;
;
②若非零向量![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,则有
,则有![]() ;
;
③若![]() ,
,![]() ,
,![]() 是空间的一组基底,且
是空间的一组基底,且![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
④若向量![]() ,
,![]() ,
,![]() ,是空间一组基底,则
,是空间一组基底,则![]() ,
,![]() ,
,![]() 也是空间的一组基底.
也是空间的一组基底.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地需要修建一条大型输油管道通过720千米宽的荒漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为108万元,铺设距离为![]() 千米的相邻两增压站之间的输油管道费用为
千米的相邻两增压站之间的输油管道费用为![]() 万元.设余下工程的总费用为
万元.设余下工程的总费用为![]() 万元.
万元.
(1)试将![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(2)需要修建多少个增压站才能使总费用![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱椎P-ABCD中,底面ABCD的边长为2,侧棱长为![]() .
.

(I)若点E为PD上的点,且PB∥平面EAC.试确定E点的位置;
(Ⅱ)在(I)的条件下,点F为线段PA上的一点且![]() ,若平面AEC和平面BDF所成的锐二面角的余弦值为
,若平面AEC和平面BDF所成的锐二面角的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com