
【题目】已知函数![]() (
(![]() ).
).
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的极值点个数.
的极值点个数.
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() 只有一个极大值点;当
只有一个极大值点;当![]() 时,
时,![]() 有一个极大值点和一个极小值点
有一个极大值点和一个极小值点
【解析】
(1)将点坐标代入函数解析式,求得参数![]() 的值,代入导函数即可求得切线的斜率,进而求得切线方程.
的值,代入导函数即可求得切线的斜率,进而求得切线方程.
(2)求得导函数并化简变形,进而讨论![]() 、
、![]() 、
、![]() 三种情况,结合函数的单调性即可确定极值情况.
三种情况,结合函数的单调性即可确定极值情况.
(1)函数![]() 图象过点
图象过点![]() ,
,
代入可得![]() ,
,
∴解得![]() .
.
代入函数可得![]() ,
,
则![]() ,
,
所以![]() ,
,
由点斜式可得切线方程为![]() .
.
所以函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)函数![]() (
(![]() ).
).
则![]() ,
,![]() ,
,
令![]() ,
,![]() .
.
(ⅰ)当![]() 时,代入可得
时,代入可得![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() ,
,![]() ,所以函数
,所以函数![]() 在
在![]() 内单调递增,
内单调递增,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递减,
时单调递减,
因而![]() 只有一个极大值点
只有一个极大值点![]()
(ⅱ)当![]() 时,令
时,令![]() ,
,
由两根之积为![]() 可知方程只有一个正根
可知方程只有一个正根![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 单调递减,
单调递减,
因而![]() 只有一个极大值点
只有一个极大值点![]()
(ⅲ)当![]() 时,令
时,令![]() ,有两个正根
,有两个正根![]() ,
,
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 增 | 极大值 | 减 | 极小值 | 增 |
综上可知,当![]() 时,
时,![]() 只有一个极大值点;
只有一个极大值点;
当![]() 时,
时,![]() 有一个极大值点和一个极小值点.
有一个极大值点和一个极小值点.


科目:高中数学 来源: 题型:
【题目】京广高速铁路(又称京广高铁)是中国运营中的高速客运专线之一,被誉为世界上运营里程最长的高速铁路,在出行人群中越来越受欢迎.现交通部门利用大数据工具随机抽取了沿线城市出行人群中的![]() 名旅客进行调查统计,得知在这
名旅客进行调查统计,得知在这![]() 名旅客中
名旅客中![]() 岁(含)以下采用乘坐京广高铁出行的占
岁(含)以下采用乘坐京广高铁出行的占![]() .
.
|
| 合计 | |
乘京广高跌 |
| ||
不乘京广高跌 | |||
合计 |
|
|
(1)请完成的![]() 列联表,并由列联表中所得数据判断有多大把握认为“乘坐京广高铁出行与年龄有关”?
列联表,并由列联表中所得数据判断有多大把握认为“乘坐京广高铁出行与年龄有关”?
(2)为优化服务质量,铁路部门从这![]() 名旅客按年龄采用分层抽样的方法随机抽取
名旅客按年龄采用分层抽样的方法随机抽取![]() 人免费到广州参加座谈会,会后再进行抽奖活动,奖品共三份.由于年龄差异,规定
人免费到广州参加座谈会,会后再进行抽奖活动,奖品共三份.由于年龄差异,规定![]() 岁(含)以下的旅客若中奖每人得
岁(含)以下的旅客若中奖每人得![]() 元,
元,![]() 岁以上的旅客若中奖每人得
岁以上的旅客若中奖每人得![]() 元,这两个年龄段的得奖人数分别记为
元,这两个年龄段的得奖人数分别记为![]() 与
与![]() .设旅客抽奖所得的总金额为
.设旅客抽奖所得的总金额为![]() 元,求
元,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
参考公式: 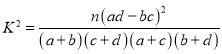 ,
,![]() 参考数据如表
参考数据如表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 是面对角线
是面对角线![]() 上两个不同的动点.以下四个命题:①存在
上两个不同的动点.以下四个命题:①存在![]() 两点,使
两点,使![]() ;②存在
;②存在![]() 两点,使
两点,使![]() 与直线
与直线![]() 都成
都成![]() 的角;③若
的角;③若![]() ,则四面体
,则四面体![]() 的体积一定是定值;④若
的体积一定是定值;④若![]() ,则四面体
,则四面体![]() 在该正方体六个面上的正投影的面积的和为定值.其中为真命题的是____.
在该正方体六个面上的正投影的面积的和为定值.其中为真命题的是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=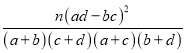 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足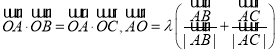 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com