
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.

(1)若![]() 为
为![]() 上一点,且
上一点,且![]() ,证明:平面
,证明:平面![]() 平面
平面![]() .
.
(2)若![]() 为棱
为棱![]() 上一点,且
上一点,且![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)由![]() 平面
平面![]() 可得
可得![]() ,又
,又![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,根据面面垂直的判定定理得平面
,根据面面垂直的判定定理得平面![]() 平面
平面![]() 。(2)在
。(2)在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,根据勾股定理可得AB=3,BC=1,PB=2,由
,根据勾股定理可得AB=3,BC=1,PB=2,由![]() 平面
平面![]() 可得
可得![]() ,从而得到
,从而得到![]() ,故BD=1.过
,故BD=1.过![]() 作
作![]() ,交
,交![]() 于
于![]() ,则
,则![]() 为三棱锥
为三棱锥![]() 的高,且
的高,且![]() 由三棱锥的体积公式可得
由三棱锥的体积公式可得![]() 。
。
试题解析:
(1)证明:∵ ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴ 平面![]() 平面
平面![]() .
.
(2)解:
在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,
,
∴![]() ,
,
由条件得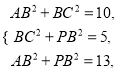 解得
解得 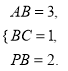
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() .
.
过![]() 作
作![]() ,交img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/18/b0e15a69/SYS201712291828428337502978_DA/SYS201712291828428337502978_DA.053.png" width="28" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于
,交img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/18/b0e15a69/SYS201712291828428337502978_DA/SYS201712291828428337502978_DA.053.png" width="28" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于![]() ,则
,则![]() 为三棱锥
为三棱锥![]() 的高,则
的高,则![]() .
.
∵![]() ,
,
∴ ![]() .
.
即三棱锥![]() 的体积为
的体积为![]() 。
。


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
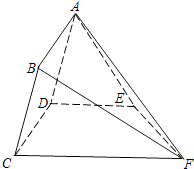
【题目】如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2, ![]() ,CF=6,∠CFE=45°.
,CF=6,∠CFE=45°.
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)在线段CF上求一点G,使锐二面角B﹣EG﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,A,B两点5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为ξ,则P(ξ≥8)= . 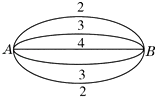
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
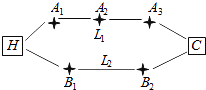
【题目】如图,李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为 ![]() ,
, ![]() .
. 
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点. 
(1)求证:EF∥面PBC
(2)求证:平面PBC⊥平面PAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com