
 .
. .求证:对于任意直线L,数量积
.求证:对于任意直线L,数量积 是定值,并求出该定值.
是定值,并求出该定值.
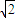 .由此能求出其方程.
.由此能求出其方程.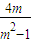 ,y1y2=
,y1y2= .
.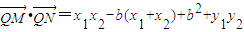 =(m2+1)y1y2+m(2-b)(y1+y2)+4-4b+b2为定值,由此得到证明.
=(m2+1)y1y2+m(2-b)(y1+y2)+4-4b+b2为定值,由此得到证明.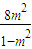 ,由此能求出|QM|2+|QN|2-|MN|2的值.
,由此能求出|QM|2+|QN|2-|MN|2的值.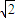 .
.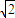 ,∴c2=2a2,a=1,方程为x2-y2=1.
,∴c2=2a2,a=1,方程为x2-y2=1.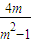 ,y1y2=
,y1y2=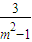 .
.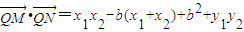
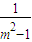 (b2-4b+1)=C(定值)…(*)
(b2-4b+1)=C(定值)…(*)  ,b=
,b= .
.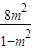 ,
, ,b=
,b= ,代入(*)式,得m2=2,
,代入(*)式,得m2=2,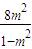 =-16.
=-16.

科目:高中数学 来源: 题型:
 (2008•奉贤区二模)如图:中心为原点的双曲线的一条渐近线为y=x,焦点A、B在x轴上,焦距|AB|为2
(2008•奉贤区二模)如图:中心为原点的双曲线的一条渐近线为y=x,焦点A、B在x轴上,焦距|AB|为2| 2 |
| 1 |
| 2 |
| QM |
| QN |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省高三年级暑期检测数学试卷(解析版) 题型:填空题
已知对称中心为原点的双曲线 与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________.
与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:中心为原点的双曲线的一条渐近线为y=x,焦点A、B在x轴上,焦距|AB|为
如图:中心为原点的双曲线的一条渐近线为y=x,焦点A、B在x轴上,焦距|AB|为 .
.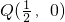 .求证:对于任意直线L,数量积
.求证:对于任意直线L,数量积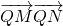 是定值,并求出该定值.
是定值,并求出该定值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com