
ΓΨΧβΡΩΓΩΡ≥–ΘΗΏ“ΜΘ®1Θ©Αύ”–Ρ–Ά§―ß45ΟϊΘ§≈°Ά§―ß15ΟϊΘ§άœ ΠΑ¥’’Ζ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ4»ΥΉιΫ®ΝΥ“ΜΗωΩΈΆβ–Υ»Λ–ΓΉι.
Θ®IΘ©«σΩΈΆβ–Υ»Λ–ΓΉι÷–Ρ–ΓΔ≈°Ά§―ßΒΡ»Υ ΐΘΜ
Θ®IIΘ©Ψ≠Ιΐ“ΜΗω‘¬ΒΡ―ßœΑΓΔΧ÷¬έΘ§’βΗω–Υ»Λ–ΓΉιΨωΕ®―Γ≥ωΝΫΟϊΆ§―ßΉωΡ≥œν Β―ιΘ§ΖΫΖ® «¥”–ΓΉιάο―Γ≥ω“ΜΟϊΆ§―ßΉω Β―ιΘ§ΗΟΆ§―ßΉωΆξΚσΘ§‘Ό¥”–ΓΉιΡΎ Θœ¬ΒΡΆ§―ß÷–―Γ≥ω“ΜΟϊΆ§―ßΉω Β―ιΘ§«σ―Γ≥ωΒΡΝΫΟϊΆ§―ß÷–«Γ”–“ΜΟϊ≈°Ά§―ßΒΡΗ≈¬ ΘΜ
Θ®IIIΘ©‘ΎΘ®IIΘ©ΒΡΧθΦΰœ¬Θ§ΒΎ“Μ¥ΈΉω Β―ιΒΡΆ§―ßAΒΟΒΫΒΡ Β―ι ΐΨίΈΣ38,40,41,42,44Θ§ΒΎΕΰ¥ΈΉω Β―ιΒΡΆ§―ßBΒΟΒΫΒΡ Β―ι ΐΨίΈΣ39,40,40,42,44Θ§«κΈ ΡΡΈΜΆ§―ßΒΡ Β―ιΗϋΈ»Ε®ΘΩ≤ΔΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©Ρ–Ά§―ßΒΡ»Υ ΐΈΣ3ΓΔ≈°Ά§―ßΒΡ»Υ ΐΖ÷±πΈΣ1; Θ®ΔρΘ©![]() ;Θ®ΔσΘ©Ά§―ßBΒΡ Β―ιΗϋΈ»Ε®.
;Θ®ΔσΘ©Ά§―ßBΒΡ Β―ιΗϋΈ»Ε®.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®IΘ©Α¥’’Ζ÷≤ψ≥ι―υΒΡΑ¥±»άΐ≥ι»ΓΒΡΖΫΖ®Θ§Ρ–≈°…ζ≥ι»ΓΒΡ±»άΐ «45ΘΚ15Θ§4»Υ÷–ΒΡΡ–≈°≥ι»Γ±»άΐ“≤ «![]() Θ§¥”ΕχΫβΨωΘΜ
Θ§¥”ΕχΫβΨωΘΜ
Θ®IIΘ©œ»Υψ≥ω―Γ≥ωΒΡΝΫΟϊΆ§―ßΒΡΜυ±Ψ ¬Φΰ ΐΘ§”–Θ®![]() Θ§Ι≤6÷÷ΘΜ‘ΌΥψ≥ω«Γ”–“ΜΟϊ≈°Ά§―ß ¬Φΰ ΐΘ§ΝΫ’Ώ±»÷ΒΦ¥ΈΣΥυ«σΗ≈¬ ΘΜ
Θ§Ι≤6÷÷ΘΜ‘ΌΥψ≥ω«Γ”–“ΜΟϊ≈°Ά§―ß ¬Φΰ ΐΘ§ΝΫ’Ώ±»÷ΒΦ¥ΈΣΥυ«σΗ≈¬ ΘΜ
Θ®IIIΘ©”ϊΈ ΡΡΈΜΆ§―ßΒΡ ‘―ιΗϋΈ»Ε®Θ§÷Μ“ΣΥψ≥ωΥϊΟ«ΗςΉ‘ΒΡΖΫ≤ν±»Ϋœ¥σ–ΓΦ¥Ω…Θ§ΖΫ≤ν–Γ–©ΒΡ±»ΫœΈ»Ε®Θ°
‘ΧβΫβΈωΘΚ
Θ®ΔώΘ©…ηΩΈΆβ–Υ»Λ–ΓΉι÷–”–![]() ΟϊΡ–Ά§―ßΘ§
ΟϊΡ–Ά§―ßΘ§
‘ρ![]() ΫβΒΟ
ΫβΒΟ![]() =3Θ§
=3Θ§
Υυ“‘Ρ–Ά§―ßΒΡ»Υ ΐΈΣ3ΓΔ≈°Ά§―ßΒΡ»Υ ΐΖ÷±πΈΣ1.
Θ®ΔρΘ©Α―»ΐΟϊΡ–Ά§―ßΚΆ“ΜΟϊ≈°Ά§―ßΖ÷±πΦ«ΈΣ![]() ‘ρ―Γ»ΓΝΫΟϊΆ§―ßœ»ΚσΉω Β―ιΒΡΜυ±Ψ ¬Φΰ”–ΘΚ
‘ρ―Γ»ΓΝΫΟϊΆ§―ßœ»ΚσΉω Β―ιΒΡΜυ±Ψ ¬Φΰ”–ΘΚ ![]()
![]()
![]()
![]() Ι≤12÷÷Θ§
Ι≤12÷÷Θ§
Τδ÷–”–“ΜΟϊ≈°Ά§―ßΒΡ«ιΩω”–6÷÷Θ§
Υυ“‘―Γ≥ωΒΡΝΫΟϊΆ§―ß÷–«Γ”–“ΜΟϊ≈°Ά§―ßΒΡΗ≈¬ ΈΣ![]()
Θ®ΔσΘ©”…Χβ÷ΣΘ§ ![]()
![]()
![]() Θ§
Θ§
![]()
![]() Ι Ά§―ßBΒΡ Β―ιΗϋΈ»Ε®.
Ι Ά§―ßBΒΡ Β―ιΗϋΈ»Ε®.


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=Θ®![]() Θ©x.
Θ©x.
Θ®ΔώΘ©Β±xΓ [©¹1Θ§1] ±Θ§«σΚ· ΐy=[fΘ®xΘ©]2©¹2afΘ®xΘ©+3ΒΡΉν–Γ÷ΒgΘ®aΘ©ΘΜ
Θ®ΔρΘ©‘ΎΘ®ΔώΘ©ΒΡΧθΦΰœ¬Θ§ «Ζώ¥φ‘Ύ Β ΐmΘΨnΘΨ3Θ§ ΙΒΟgΘ®xΘ©ΒΡΕ®“ε”ρΈΣ[nΘ§m]Θ§÷Β”ρΈΣ[n2Θ§m2]ΘΩ»τ¥φ‘ΎΘ§«σ≥ωmΓΔnΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡάβΉΕ![]() ΒΡΒΉΟφ
ΒΡΒΉΟφ![]() «ΨΊ–ΈΘ§ΤΫΟφ
«ΨΊ–ΈΘ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() «
«![]() ΒΡ÷–ΒψΘ§«“
ΒΡ÷–ΒψΘ§«“![]() Θ§
Θ§![]() .
.
Θ®IΘ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®IIΘ©«σ»ΐάβΉΕ![]() ΒΡΧεΜΐ.
ΒΡΧεΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
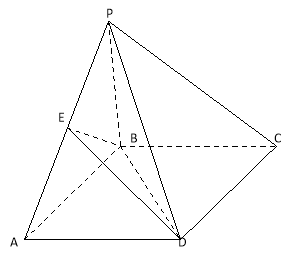
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕP©¹ABCD÷–Θ§ΤΫΟφPADΓΆΤΫΟφABCDΘ§ABΓΈDCΘ§ΓςPAD «Β»±Ώ»ΐΫ«–ΈΘ§“―÷ΣAD=4Θ§ ![]() Θ§AB=2CD=8Θ°
Θ§AB=2CD=8Θ°
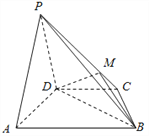
Θ®1Θ©…ηM «PC…œΒΡ“ΜΒψΘ§÷ΛΟςΘΚΤΫΟφMBDΓΆΤΫΟφPADΘΜ
Θ®2Θ©Β±MΒψΈΜ”ΎœΏΕΈPC ≤Ο¥ΈΜ÷Ο ±Θ§PAΓΈΤΫΟφMBDΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗυΨίΙζΦ“ΜΖ±Θ≤Ω–¬–όΕ©ΒΡΓΕΜΖΨ≥Ω’Τχ÷ ΝΩ±ξΉΦΓΖΙφΕ®ΘΚΨ”Οώ«χ![]() ΒΡΡξΤΫΨυ≈®Ε»≤ΜΒΟ≥§Ιΐ
ΒΡΡξΤΫΨυ≈®Ε»≤ΜΒΟ≥§Ιΐ![]() ΈΔΩΥ/ΝΔΖΫΟΉΘ§
ΈΔΩΥ/ΝΔΖΫΟΉΘ§![]() ΒΡ24–Γ ±ΤΫΨυ≈®Ε»≤ΜΒΟ≥§Ιΐ
ΒΡ24–Γ ±ΤΫΨυ≈®Ε»≤ΜΒΟ≥§Ιΐ![]() ΈΔΩΥ/ΝΔΖΫΟΉΘ°Ρ≥≥« –ΜΖ±Θ≤ΩΟ≈ΥφΜζ≥ι»ΓΝΥ“ΜΨ”Οώ«χ»ΞΡξ20Χλ
ΈΔΩΥ/ΝΔΖΫΟΉΘ°Ρ≥≥« –ΜΖ±Θ≤ΩΟ≈ΥφΜζ≥ι»ΓΝΥ“ΜΨ”Οώ«χ»ΞΡξ20Χλ![]() ΒΡ24–Γ ±ΤΫΨυ≈®Ε»ΒΡΦύ≤β ΐΨίΘ§ ΐΨίΆ≥ΦΤ»γœ¬ΘΚ
ΒΡ24–Γ ±ΤΫΨυ≈®Ε»ΒΡΦύ≤β ΐΨίΘ§ ΐΨίΆ≥ΦΤ»γœ¬ΘΚ
Ήι±π |
Θ®ΈΔΩΥ/ΝΔΖΫΟΉΘ© | ΤΒ ΐΘ®ΧλΘ© | ΤΒ¬ |
ΒΎ“ΜΉι |
| 3 | 0.15 |
ΒΎΕΰΉι |
| 12 | 0.6 |
ΒΎ»ΐΉι |
| 3 | 0.15 |
ΒΎΥΡΉι |
| 2 | 0.1 |
Θ®1Θ©¥”―υ±Ψ÷–![]() ΒΡ24–Γ ±ΤΫΨυ≈®Ε»≥§Ιΐ50ΈΔΩΥ/ΝΔΖΫΟΉΒΡ5Χλ÷–Θ§ΥφΜζ≥ι»Γ2ΧλΘ§«σ«ΓΚΟ”–“ΜΧλ
ΒΡ24–Γ ±ΤΫΨυ≈®Ε»≥§Ιΐ50ΈΔΩΥ/ΝΔΖΫΟΉΒΡ5Χλ÷–Θ§ΥφΜζ≥ι»Γ2ΧλΘ§«σ«ΓΚΟ”–“ΜΧλ
![]() ΒΡ24–Γ ±ΤΫΨυ≈®Ε»≥§Ιΐ75ΈΔΩΥ/ΝΔΖΫΟΉΒΡΗ≈¬ ΘΜ
ΒΡ24–Γ ±ΤΫΨυ≈®Ε»≥§Ιΐ75ΈΔΩΥ/ΝΔΖΫΟΉΒΡΗ≈¬ ΘΜ
Θ®2Θ©«σ―υ±ΨΤΫΨυ ΐΘ§≤ΔΗυΨί―υ±ΨΙάΦΤΉήΧεΒΡΥΦœκΘ§¥”![]() ΒΡΡξΤΫΨυ≈®Ε»ΩΦ¬«Θ§≈–ΕœΗΟΨ”Οώ«χΒΡΜΖΨ≥ «
ΒΡΡξΤΫΨυ≈®Ε»ΩΦ¬«Θ§≈–ΕœΗΟΨ”Οώ«χΒΡΜΖΨ≥ «
Ζώ–η“ΣΗΡΫχΘΩΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ»γΆΦΥυ ΨΒΡ»ΐάβΉΕ![]() ÷–Θ§
÷–Θ§![]() Ζ÷±π «
Ζ÷±π «![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
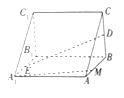
Θ®1Θ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() ΈΣ’ΐ»ΐΫ«–ΈΘ§«“
ΈΣ’ΐ»ΐΫ«–ΈΘ§«“![]() ΈΣ
ΈΣ![]() …œΒΡ“ΜΒψΘ§
…œΒΡ“ΜΒψΘ§![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() Υυ≥…Ϋ«ΒΡ’ΐ«–÷ΒΘ°
Υυ≥…Ϋ«ΒΡ’ΐ«–÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΕύΟφΧε![]() ÷–Θ§Οφ
÷–Θ§Οφ![]() ΈΣΨΊ–ΈΘ§
ΈΣΨΊ–ΈΘ§![]() Θ§«“
Θ§«“![]() Θ°
Θ°
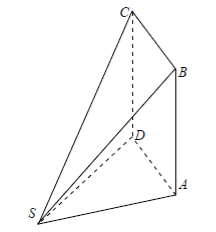
Θ®1Θ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ![]() ”κ
”κ![]() Υυ≥…Ϋ«ΒΡ”ύœ“÷ΒΘΜ
Υυ≥…Ϋ«ΒΡ”ύœ“÷ΒΘΜ
Θ®3Θ©«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷ΒΘ°
ΒΡ”ύœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΚ· ΐf(x)ΘΫ![]() ΈΣΤφΚ· ΐΘ°
ΈΣΤφΚ· ΐΘ°
(1) «σaΒΡ÷ΒΘΜ
(2) ≈–Εœf(x)ΒΡΒΞΒς–‘Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΤΫ––ΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§«“Γς
ΒΡ÷–ΒψΘ§«“Γς![]() «Β»±Ώ»ΐΫ«–ΈΘ§―Ί
«Β»±Ώ»ΐΫ«–ΈΘ§―Ί![]() Α―Γς
Α―Γς![]() ’έΤπ÷Ν
’έΤπ÷Ν![]() ΒΡΈΜ÷ΟΘ§ ΙΒΟ
ΒΡΈΜ÷ΟΘ§ ΙΒΟ![]() Θ°
Θ°
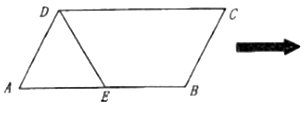
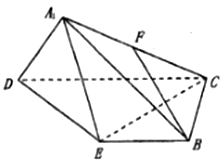
Θ®1Θ©![]() «œΏΕΈ
«œΏΕΈ![]() ΒΡ÷–ΒψΘ§«σ÷ΛΘΚ
ΒΡ÷–ΒψΘ§«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©«σΒψ![]() ΒΫΤΫΟφ
ΒΫΤΫΟφ![]() ΒΡΨύάκΘ°
ΒΡΨύάκΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com