
【题目】2018年俄罗斯世界杯共有32支球队参赛,将32支球队分为8个小组,每个小组有4支球队,各个小组首先进行小组赛,小组赛采用单循环制,即小组内的每支球队都与本小组的其他球队进行一场比赛,球迷小王喜欢的4支球队分别为西班牙队、法国队、德国队和韩国队,其中西班牙队在B组,法国队在C组,德国队和韩国队同在F组.小王要从自己喜欢的4支球队的所有小组赛中,选择5场比赛观看,则至少观看2场法国队比赛的方法有_____________种.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()

(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
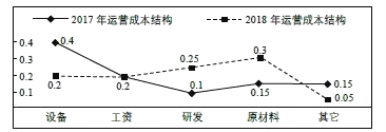
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惰性气体分子为单原子分子,在自由原子情形下,其电子电荷分布是球对称的.负电荷中心与原子核重合,但如两个原子接近,则彼此能因静电作用产生极化(正负电荷中心不重合),从而导致有相互作用力,这称为范德瓦尔斯相互作用.今有两个相同的惰性气体原子,它们的原子核固定,原子核正电荷的电荷量为![]() ,这两个相距为
,这两个相距为![]() 的惰性气体原子组成体系的能量中有静电相互作用能
的惰性气体原子组成体系的能量中有静电相互作用能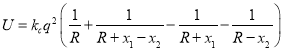 ,其中
,其中![]() 为静电常量,
为静电常量,![]() ,
,![]() 分别表示两个原子负电中心相对各自原子核的位移,且
分别表示两个原子负电中心相对各自原子核的位移,且![]() 和
和![]() 都远小于
都远小于![]() ,当
,当![]() 远小于1时,
远小于1时,![]() ,则
,则![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药开发公司实验室有![]() 瓶溶液,其中
瓶溶液,其中![]() 瓶中有细菌
瓶中有细菌![]() ,现需要把含有细菌
,现需要把含有细菌![]() 的溶液检验出来,有如下两种方案:
的溶液检验出来,有如下两种方案:
方案一:逐瓶检验,则需检验![]() 次;
次;
方案二:混合检验,将![]() 瓶溶液分别取样,混合在一起检验,若检验结果不含有细菌
瓶溶液分别取样,混合在一起检验,若检验结果不含有细菌![]() ,则
,则![]() 瓶溶液全部不含有细菌
瓶溶液全部不含有细菌![]() ;若检验结果含有细菌
;若检验结果含有细菌![]() ,就要对这
,就要对这![]() 瓶溶液再逐瓶检验,此时检验次数总共为
瓶溶液再逐瓶检验,此时检验次数总共为![]() .
.
(1)假设![]() ,采用方案一,求恰好检验3次就能确定哪两瓶溶液含有细菌
,采用方案一,求恰好检验3次就能确定哪两瓶溶液含有细菌![]() 的概率;
的概率;
(2)现对![]() 瓶溶液进行检验,已知每瓶溶液含有细菌
瓶溶液进行检验,已知每瓶溶液含有细菌![]() 的概率均为
的概率均为![]() .
.
若采用方案一.需检验的总次数为![]() ,若采用方案二.需检验的总次数为
,若采用方案二.需检验的总次数为![]() .
.
(i)若![]() 与
与![]() 的期望相等.试求
的期望相等.试求![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ;
;
(ii)若![]() ,且采用方案二总次数的期望小于采用方案一总次数的期望.求
,且采用方案二总次数的期望小于采用方案一总次数的期望.求![]() 的最大值.
的最大值.
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的等边△ABC中,D,E分别为边AC,AB的中点.将△ADE沿DE折起,使得AB⊥AD,得到如图2的四棱锥A﹣BCDE,连结BD,CE,且BD与CE交于点H.
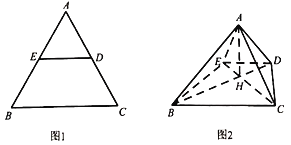
(1)证明:![]() ;
;
(2)设点B到平面AED的距离为h1,点E到平面ABD的距离为h2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海、香港、澳门三地,大大缩短了三地的时空距离,盘活了珠江三角洲的经济,被誉为新的世界七大奇迹.截至2019年10月23日8点,珠海公路口岸共验放出入境旅客超过1400万人次,日均客流量已经达到4万人次,验放出入境车辆超过70万辆次,2019年春节期间,客流再次大幅增长,日均客流达8万人次,单日客流量更是创下11.3万人次的最高纪录.2019年从五月一日开始的连续100天客流量频率分布直方图如图.
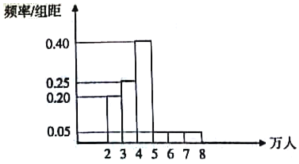
(1)求这100天中,客流量超过4万的频率;
(2)①同一组数据用该区间的中点值代替,根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com