
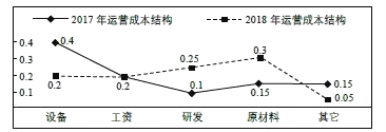
ΓΨΧβΡΩΓΩΡ≥Τσ“Β“ΐΫχœ÷¥ζΜ·ΙήάμΧε÷ΤΘ§…ζ≤ζ–ß“φΟςœ‘ΧαΗΏ.2018Ρξ»ΪΡξΉή ’»κ”κ2017Ρξ»ΪΡξΉή ’»κœύ±»‘ω≥ΛΝΥ“Μ±ΕΘ§ Βœ÷Ζ≠Ζ§.Ά§ ±ΗΟΤσ“ΒΒΡΗςœν‘Υ”Σ≥…±Ψ“≤ΥφΉ≈ ’»κΒΡ±δΜ·ΖΔ…ζΝΥœύ”Π±δΜ·.œ¬ΆΦΗχ≥ωΝΥΗΟΤσ“Β’βΝΫΡξ≤ΜΆ§‘Υ”Σ≥…±Ψ’Φ»ΪΡξΉή ’»κΒΡ±»άΐΘ§œ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©
A.ΗΟΤσ“Β2018Ρξ‘≠≤ΡΝœΖ―”Ο «2017ΡξΙΛΉ ΫπΕν”κ―–ΖΔΖ―”ΟΒΡΚΆ
B.ΗΟΤσ“Β2018Ρξ―–ΖΔΖ―”Ο «2017ΡξΙΛΉ ΫπΕνΓΔ‘≠≤ΡΝœΖ―”ΟΓΔΤδΥϋΖ―”Ο»ΐœνΒΡΚΆ
C.ΗΟΤσ“Β2018ΡξΤδΥϋΖ―”Ο «2017ΡξΙΛΉ ΫπΕνΒΡ![]()
D.ΗΟΤσ“Β2018Ρξ…η±ΗΖ―”Ο «2017Ρξ‘≠≤ΡΝœΒΡΖ―”ΟΒΡΝΫ±Ε
ΓΨ¥πΑΗΓΩB
ΓΨΫβΈωΓΩ
œ»Ε‘’έœΏΆΦ–≈œΔΒΡάμΫβΦΑ¥ΠάμΘ§‘ΌΫαΚœ ΐΨίΫχ––ΦρΒΞΒΡΚœ«ιΆΤάμ÷π“ΜΦλ―ιΦ¥Ω…ΒΟΫβΘ°
ΫβΘΚ”…’έœΏΆΦΩ…÷ΣΘΚ≤ΜΖΝ…η2017Ρξ»ΪΡξΒΡ ’»κΈΣtΘ§‘ρ2018Ρξ»ΪΡξΒΡ ’»κΈΣ2t.
Ε‘”Ύ―ΓœνAΘ§ΗΟΤσ“Β2018Ρξ‘≠≤ΡΝœΖ―”ΟΈΣ0.3ΓΝ2tΘΫ0.6tΘ§2017ΡξΙΛΉ ΫπΕν”κ―–ΖΔΖ―”ΟΒΡΚΆΈΣ0.2t+0.1tΘΫ0.3tΘ§Ι A¥μΈσΘΜ
Ε‘”Ύ―ΓœνBΘ§ΗΟΤσ“Β2018Ρξ―–ΖΔΖ―”ΟΈΣ0.25ΓΝ2tΘΫ0.5tΘ§2017ΡξΙΛΉ ΫπΕνΓΔ‘≠≤ΡΝœΖ―”ΟΓΔΤδΥϋΖ―”Ο»ΐœνΒΡΚΆΈΣ0.2t+0.15t+0.15tΘΫ0.5tΘ§Ι B’ΐ»ΖΘΜ
Ε‘”Ύ―ΓœνCΘ§ΗΟΤσ“Β2018ΡξΤδΥϋΖ―”Ο «0.05ΓΝ2tΘΫ0.1tΘ§2017ΡξΙΛΉ ΫπΕν «0.2tΘ§Ι C¥μΈσΘΜ
Ε‘”Ύ―ΓœνDΘ§ΗΟΤσ“Β2018Ρξ…η±ΗΖ―”Ο «0.2ΓΝ2tΘΫ0.4tΘ§2017Ρξ‘≠≤ΡΝœΒΡΖ―”Ο «0.15tΘ§Ι D¥μΈσ.
Ι ―ΓΘΚ![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ «±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈΘ§
÷–Θ§ΒΉΟφ «±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈΘ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§Βψ
÷–ΒψΘ§Βψ![]() ‘Ύ
‘Ύ![]() …œ«“
…œ«“![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() ‘Ύ
‘Ύ![]() ―”≥ΛœΏ…œΘ§
―”≥ΛœΏ…œΘ§![]() Θ§ΫΜ
Θ§ΫΜ![]() ”Ύ
”Ύ![]() Θ§«“
Θ§«“![]()

(1)÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
(2)…ηΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§»τΕΰΟφΫ«
…œΘ§»τΕΰΟφΫ«![]() ΈΣ
ΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΒΡΫΙΒψΈΣFΘ§Βψ
ΒΡΫΙΒψΈΣFΘ§Βψ![]() ‘Ύ¥Υ≈ΉΈοœΏ…œΘ§
‘Ύ¥Υ≈ΉΈοœΏ…œΘ§![]() Θ§≤ΜΙΐ‘≠ΒψΒΡ÷±œΏ
Θ§≤ΜΙΐ‘≠ΒψΒΡ÷±œΏ![]() ”κ≈ΉΈοœΏCΫΜ”ΎAΘ§BΝΫΒψΘ§“‘ABΈΣ÷±ΨΕΒΡ‘≤MΙΐΉχ±ξ‘≠ΒψΘ°
”κ≈ΉΈοœΏCΫΜ”ΎAΘ§BΝΫΒψΘ§“‘ABΈΣ÷±ΨΕΒΡ‘≤MΙΐΉχ±ξ‘≠ΒψΘ°
(1)«σ≈ΉΈοœΏCΒΡΖΫ≥ΧΘΜ
(2)÷ΛΟςΘΚ÷±œΏ![]() ΚψΙΐΕ®ΒψΘΜ
ΚψΙΐΕ®ΒψΘΜ
(3)»τœΏΕΈAB÷–ΒψΒΡΉίΉχ±ξΈΣ2Θ§«σ¥Υ ±÷±œΏ![]() ΚΆ‘≤MΒΡΖΫ≥ΧΘ°
ΚΆ‘≤MΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ®
Θ®![]() Θ©Θ°
Θ©Θ°
Θ®ΔώΘ©»τ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏ”κ÷±œΏ
¥ΠΒΡ«–œΏ”κ÷±œΏ![]() ¥Ι÷±Θ§«σ
¥Ι÷±Θ§«σ![]() ΒΡ÷Β”κ«ζœΏ‘ΎΒψ
ΒΡ÷Β”κ«ζœΏ‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τ![]() Θ§«“Β±
Θ§«“Β±![]() ±Θ§
±Θ§ ![]() Κψ≥…ΝΔΘ§«σ
Κψ≥…ΝΔΘ§«σ![]() ΒΡΉν¥σ÷ΒΘ°Θ®
ΒΡΉν¥σ÷ΒΘ°Θ®![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ®
Θ®![]() «“
«“![]() Θ©Θ§‘ρΙΊ”ΎxΒΡ≤ΜΒ» Ϋ
Θ©Θ§‘ρΙΊ”ΎxΒΡ≤ΜΒ» Ϋ![]() ΒΡΫβΦ· «Θ® Θ©
ΒΡΫβΦ· «Θ® Θ©
A.![]() B.
B.![]()
C.![]() D.“‘…œ¥πΑΗΕΦ≤ΜΕ‘
D.“‘…œ¥πΑΗΕΦ≤ΜΕ‘
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐ![]() .
.
Θ®1Θ©«σfΘ®xΘ©ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©Β±xΘΨ0 ±Θ§ex©¹ax2©¹x©¹aΓί0≥…ΝΔΘ§«σ’ΐ Β ΐaΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΤΫΟφ![]() ΦΑ÷±œΏ
ΦΑ÷±œΏ![]() Θ§
Θ§![]() Θ§‘ρœ¬Ν–ΥΒΖ®¥μΈσΒΡΗω ΐ «Θ® Θ©Θ°
Θ§‘ρœ¬Ν–ΥΒΖ®¥μΈσΒΡΗω ΐ «Θ® Θ©Θ°
ΔΌ»τ÷±œΏ![]() Θ§
Θ§![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΕΦ «
Υυ≥…Ϋ«ΕΦ «![]() Θ§‘ρ’βΝΫΧθ÷±œΏΤΫ––ΘΜΔΎ»τ÷±œΏ
Θ§‘ρ’βΝΫΧθ÷±œΏΤΫ––ΘΜΔΎ»τ÷±œΏ![]() Θ§
Θ§![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΕΦ «
Υυ≥…Ϋ«ΕΦ «![]() Θ§‘ρ’βΝΫΧθ÷±œΏ≤ΜΩ…Ρή¥Ι÷±ΘΜΔέ»τ÷±œΏ
Θ§‘ρ’βΝΫΧθ÷±œΏ≤ΜΩ…Ρή¥Ι÷±ΘΜΔέ»τ÷±œΏ![]() Θ§
Θ§![]() ¥Ι÷±Θ§‘ρ’βΝΫΧθ÷±œΏ”κΤΫΟφ
¥Ι÷±Θ§‘ρ’βΝΫΧθ÷±œΏ”κΤΫΟφ![]() ≤ΜΩ…ΡήΕΦ¥Ι÷±ΘΜΔή»τ÷±œΏ
≤ΜΩ…ΡήΕΦ¥Ι÷±ΘΜΔή»τ÷±œΏ![]() Θ§
Θ§![]() ΤΫ––Θ§‘ρ’βΝΫΧθ÷±œΏ÷–÷Ν…Ό”–“ΜΧθ”κΤΫΟφ
ΤΫ––Θ§‘ρ’βΝΫΧθ÷±œΏ÷–÷Ν…Ό”–“ΜΧθ”κΤΫΟφ![]() ΤΫ––Θ°
ΤΫ––Θ°
A.1B.2C.3D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2018ΡξΕμ¬όΥΙ άΫγ±≠Ι≤”–32÷ß«ρΕ”≤Έ»ϋΘ§ΫΪ32÷ß«ρΕ”Ζ÷ΈΣ8Ηω–ΓΉιΘ§ΟΩΗω–ΓΉι”–4÷ß«ρΕ”Θ§ΗςΗω–ΓΉι Ήœ»Ϋχ–––ΓΉι»ϋΘ§–ΓΉι»ϋ≤…”ΟΒΞ―≠ΜΖ÷ΤΘ§Φ¥–ΓΉιΡΎΒΡΟΩ÷ß«ρΕ”ΕΦ”κ±Ψ–ΓΉιΒΡΤδΥϊ«ρΕ”Ϋχ––“Μ≥Γ±»»ϋΘ§«ρΟ‘–ΓΆθœ≤ΜΕΒΡ4÷ß«ρΕ”Ζ÷±πΈΣΈςΑύ―άΕ”ΓΔΖ®ΙζΕ”ΓΔΒ¬ΙζΕ”ΚΆΚΪΙζΕ”Θ§Τδ÷–ΈςΑύ―άΕ”‘ΎBΉιΘ§Ζ®ΙζΕ”‘ΎCΉιΘ§Β¬ΙζΕ”ΚΆΚΪΙζΕ”Ά§‘ΎFΉι.–ΓΆθ“Σ¥”Ή‘ΦΚœ≤ΜΕΒΡ4÷ß«ρΕ”ΒΡΥυ”––ΓΉι»ϋ÷–Θ§―Γ‘ώ5≥Γ±»»ϋΙέΩ¥Θ§‘ρ÷Ν…ΌΙέΩ¥2≥ΓΖ®ΙζΕ”±»»ϋΒΡΖΫΖ®”–_____________÷÷.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]()
Θ®1Θ©»τ![]() Θ§«“
Θ§«“![]() ‘ΎΤδΕ®“ε”ρ…œ¥φ‘ΎΒΞΒςΒίΦθ«χΦδΘ§«σ Β ΐ
‘ΎΤδΕ®“ε”ρ…œ¥φ‘ΎΒΞΒςΒίΦθ«χΦδΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©…ηΚ· ΐ![]() Θ§
Θ§ ![]() Θ§»τ
Θ§»τ![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…ηΚ· ΐ![]() ΒΡΆΦœσ
ΒΡΆΦœσ![]() ”κΚ· ΐ
”κΚ· ΐ![]() ΒΡΆΦœσ
ΒΡΆΦœσ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§ΙΐœΏΕΈ
Θ§ΙΐœΏΕΈ![]() ΒΡ÷–ΒψΉς
ΒΡ÷–ΒψΉς![]() ÷αΒΡ¥ΙœΏΖ÷±πΫΜ
÷αΒΡ¥ΙœΏΖ÷±πΫΜ![]() Θ§
Θ§ ![]() ”ΎΒψ
”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§÷ΛΟςΘΚ
Θ§÷ΛΟςΘΚ ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏ”κ
¥ΠΒΡ«–œΏ”κ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏ≤ΜΤΫ––.
¥ΠΒΡ«–œΏ≤ΜΤΫ––.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com