
【题目】已知函数![]() (
(![]() 且
且![]() ),则关于x的不等式
),则关于x的不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() D.以上答案都不对
D.以上答案都不对
【答案】B
【解析】
先证明![]() 为偶函数,在
为偶函数,在![]() 上是增函数,且
上是增函数,且![]() ,已知不等式可转化为
,已知不等式可转化为![]() ,只需满足
,只需满足![]() ,计算解得对数不等式即可得出结果.
,计算解得对数不等式即可得出结果.
根据题意,函数f(x)=ax+a﹣x,其定义域为R,又由f(﹣x)=ax+a﹣x=f(x),
即函数f(x)为偶函数,
又由f′(x)=(ax﹣a﹣x)lna,
若a>1,当x∈[0,+∞)时,ax﹣a﹣x≥0且lna≥0,此时f′(x)≥0,
若0<a<1,当x∈[0,+∞)时,ax﹣a﹣x≤0且lna≤0,此时f′(x)≥0,
则当x∈[0,+∞)时,都有f′(x)≥0,即函数f(x)在[0,+∞)上为增函数,
可得![]() (
(![]() ,
,![]() )为偶函数且在
)为偶函数且在![]() 上是增函数,
上是增函数,![]() ,∴
,∴![]() ,即
,即![]() ,
,![]() ,
,![]() 或
或![]() ,解得
,解得![]() 或
或![]() .即
.即![]() .
.
故选:B.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求证:数列![]() 等差数列;
等差数列;
(2)当![]() 时,记
时,记![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)若数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是公比为
是公比为![]() 的等比数列,求最小正整数
的等比数列,求最小正整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,是以十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)形象化代表人的出生年份,现有十二生肖的吉祥物各一个,三位属相不同的小朋友依次每人选一个,则三位小朋友都不选和自己属相相同的吉祥物的选法有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点H,使得
交于点H,使得![]() 平面
平面![]() ,试确定点H的位置,并给出证明;
,试确定点H的位置,并给出证明;
(2)在(1)的条件下,若二面角![]() 的大小为
的大小为![]() ,试求直线
,试求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
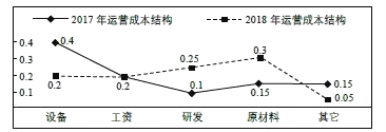
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量![]() (件)与相应的生产总成本
(件)与相应的生产总成本![]() (万元)的四组对照数据.
(万元)的四组对照数据.
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
工厂研究人员建立了![]() 与
与![]() 的两种回归模型,利用计算机算得近似结果如下:
的两种回归模型,利用计算机算得近似结果如下:
模型①:![]() ;
;
模型②:![]() .
.
其中模型①的残差(实际值预报值)图如图所示:
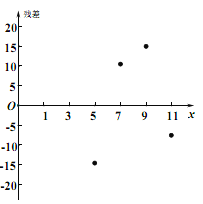
(1)根据残差分析,判断哪一个更适宜作为![]() 关于
关于![]() 的回归方程?并说明理由;
的回归方程?并说明理由;
(2)市场前景风云变幻,研究人员统计了20个月的产品销售单价,得到频数分布表如下:
销售单价分组(万元) |
|
|
|
频数 | 10 | 6 | 4 |
若以这20个月销售单价的平均值定为今后的销售单价(同一组中的数据用该组区间的中点值作代表),结合你对(1)的判断,当月产量为12件时,预测当月的利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com