
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
【答案】(1){x|![]() }(2)
}(2)![]()
【解析】
(1)原不等式等价于|x﹣1|+|x+1|<3,然后对x分类去绝对值,化为关于x的一元一次不等式求解,取并集得答案;
(2)f(x)=|x﹣a|+|x+b|≥|b+a|,当且仅当(x﹣a)(x+b)≤0时等号成立.可得f(x)的最小值为|b+a|=2.结合ab>0,得|b+a|=|a|+|b|=2,则![]() ,展开后利用基本不等式求最值.
,展开后利用基本不等式求最值.
(1)原不等式等价于|x﹣1|+|x+1|<3,
当x≥1时,可得x﹣1+x+1<3,解得1≤x![]() ;
;
当﹣1<x<1时,可得﹣x+1+x+1<3,得2<3成立;
当x≤﹣1时,可得﹣x+1﹣x﹣1<3,解得![]() x≤﹣1.
x≤﹣1.
综上所述,原不等式的解集为{x|![]() };
};
(2)f(x)=|x﹣a|+|x+b|≥|b+a|,当且仅当(x﹣a)(x+b)≤0时等号成立.
∴f(x)的最小值为|b+a|,即|b+a|=2.
又∵ab>0,∴|b+a|=|a|+|b|=2,
∴![]()
 .
.
当且仅当![]() 时,等号成立,
时,等号成立,
∴![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: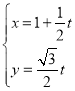 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点P是曲线
,设点P是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0)的焦点为F,直线l与抛物线C交于P,Q两点.
(1)若l过点F,抛物线C在点P处的切线与在点Q处的切线交于点G.证明:点G在定直线上.
(2)若p=2,点M在曲线y![]() 上,MP,MQ的中点均在抛物线C上,求△MPQ面积的取值范围.
上,MP,MQ的中点均在抛物线C上,求△MPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司为了解本公司快递业务情况,随机调查了100个营业网点,得到了这些营业网点2019年全年快递单数增长率x的频数分布表:

(1)分别估计该快递公司快递单数增长率不低于40%的营业网点比例和快递单数负增长的营业网点比例;
(2)求2019年该快递公司快递单数增长率的平均数和标准差的估计值(同一组中的数据用该组区间的中点值作为代表).(精确到0.01)参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面![]() 及直线
及直线![]() ,
,![]() ,则下列说法错误的个数是( ).
,则下列说法错误的个数是( ).
①若直线![]() ,
,![]() 与平面
与平面![]() 所成角都是
所成角都是![]() ,则这两条直线平行;②若直线
,则这两条直线平行;②若直线![]() ,
,![]() 与平面
与平面![]() 所成角都是
所成角都是![]() ,则这两条直线不可能垂直;③若直线
,则这两条直线不可能垂直;③若直线![]() ,
,![]() 垂直,则这两条直线与平面
垂直,则这两条直线与平面![]() 不可能都垂直;④若直线
不可能都垂直;④若直线![]() ,
,![]() 平行,则这两条直线中至少有一条与平面
平行,则这两条直线中至少有一条与平面![]() 平行.
平行.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com