
【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量![]() (件)与相应的生产总成本
(件)与相应的生产总成本![]() (万元)的四组对照数据.
(万元)的四组对照数据.
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
工厂研究人员建立了![]() 与
与![]() 的两种回归模型,利用计算机算得近似结果如下:
的两种回归模型,利用计算机算得近似结果如下:
模型①:![]() ;
;
模型②:![]() .
.
其中模型①的残差(实际值预报值)图如图所示:
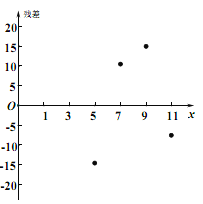
(1)根据残差分析,判断哪一个更适宜作为![]() 关于
关于![]() 的回归方程?并说明理由;
的回归方程?并说明理由;
(2)市场前景风云变幻,研究人员统计了20个月的产品销售单价,得到频数分布表如下:
销售单价分组(万元) |
|
|
|
频数 | 10 | 6 | 4 |
若以这20个月销售单价的平均值定为今后的销售单价(同一组中的数据用该组区间的中点值作代表),结合你对(1)的判断,当月产量为12件时,预测当月的利润.
【答案】(1)模型①更适宜作为![]() 关于
关于![]() 的回归方程,见解析(2)295万元.
的回归方程,见解析(2)295万元.
【解析】
(1) 模型①更适合作为y关于x的回归方程.先根据模型②: y=68x- 160逐一算出四组数据的残差, 并整理成表,再作出残差图,然后对比模型①与②,从残差的绝对值大小、残差点分布的带状区域的宽窄或残差点离x轴的远近进行理由阐述即可;
(2)先根据频数分布表算出这20个月销售单价的平均值,设月利润为![]() 万元,则
万元,则![]() ,再把x=12代入,求出z的值即可得解.
,再把x=12代入,求出z的值即可得解.
(1)模型②的残差数据如下表:
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
| 20 | -18 | -21 | 21 |
模型②的残点图如图所示.
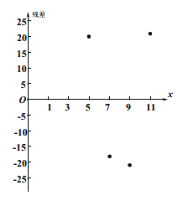
模型①更适宜作为![]() 关于
关于![]() 的回归方程,因为:
的回归方程,因为:
理由1:模型①这个4个样本点的残差的绝对值都比模型②的小.
理由2:模型①这4个样本的残差点落在的带状区域比模型②的带状区域更窄.
理由3:模型①这4个样本的残差点比模型②的残差点更贴近![]() 轴.
轴.
(2)这20个月销售单价的平均值为![]() ,
,
设月利润为![]() 万元,由题意知
万元,由题意知![]() ,
,
当![]() 时,
时,![]() (万元),
(万元),
所以当月产量为12件时,预测当月的利润为295万元.


科目:高中数学 来源: 题型:
【题目】已知⊙M过点![]() ,且与⊙N:
,且与⊙N:![]() 内切,设⊙M的圆心M的轨迹为曲线C.
内切,设⊙M的圆心M的轨迹为曲线C.
(1)求曲线C的方程:
(2)设直线l不经过点![]() 且与曲线C相交于P,Q两点.若直线PB与直线QB的斜率之积为
且与曲线C相交于P,Q两点.若直线PB与直线QB的斜率之积为![]() ,判断直线l是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.
,判断直线l是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]()
(1)若![]() ,且
,且![]() 在其定义域上存在单调递减区间,求实数
在其定义域上存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,
, ![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
, ![]() 于点
于点![]() 、
、![]() ,证明:
,证明: ![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地,大大缩短了三地的时空距离,盘活了珠江三角洲的经济,被誉为新的世界七大奇迹.截至2019年10月23日8点,珠海公路口岸共验放出入境旅客超过1400万人次,日均客流量已经达到4万人次,验放出入境车辆超过70万辆次,2019年春节期间,客流再次大幅增长,日均客流达8万人次,单日客流量更是创下11.3万人次的最高纪录.
2019年从五月一日开始的连续100天客流量频率分布直方图如下
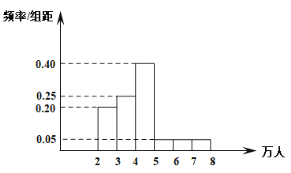
(1)①同一组数据用该区间的中点值代替,根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.
(2)设这100天中客流量超过5万人次的有![]() 天,从这
天,从这![]() 天中任取两天,设
天中任取两天,设![]() 为这两天中客流量超过7万人的天数.求
为这两天中客流量超过7万人的天数.求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为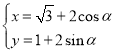 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,且长度单位相同.
轴的正半轴为极轴建立极坐标系,且长度单位相同.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() :
:![]() (
(![]() 为参数)被圆
为参数)被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com