练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，圆的参数方程为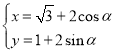（为参数），以坐标原点为极点，以轴的正半轴为极轴建立极坐标系，且长度单位相同.

    （1）求圆的极坐标方程；

    （2）若直线：（为参数）被圆截得的弦长为2，求直线的倾斜角.

    【答案】（1）；（2）或

    【解析】

    （1）根据圆的参数方程消去参数得到，然后将，代入上式得整理求解.

    （2）根据直线的参数方程消去参数得到或，再根据弦长为2，得到圆心到的距离，然后由点到直线的距离求解.

    （1）因为圆的参数方程为，

    消去参数得：，

    即，

    又因为，

    代入上式得：，

    ，

    整理得：，

    所以圆的极坐标方程为.

    （2）因为直线：，

    消去参数得：或，

    因为圆的圆心，，又弦长为2，

    所以圆心到的距离，

    当时，，

    解得，

    因为，

    所以，

    当时，，成立，

    综上：的倾斜角或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年，也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市，佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置，聚焦打造成为面向全球的国家制造业创新中心，走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下，佛山市某工厂统筹各类资源，进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量（件）与相应的生产总成本（万元）的四组对照数据.

    5

    7

    9

    11

    200

    298

    431

    609

    工厂研究人员建立了与的两种回归模型，利用计算机算得近似结果如下：

    模型①：；

    模型②：.

    其中模型①的残差（实际值预报值）图如图所示：

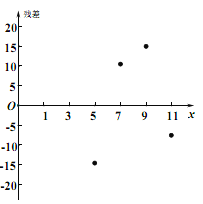
    （1）根据残差分析，判断哪一个更适宜作为关于的回归方程？并说明理由；

    （2）市场前景风云变幻，研究人员统计了20个月的产品销售单价，得到频数分布表如下：

    销售单价分组（万元）

    频数

    10

    6

    4

    若以这20个月销售单价的平均值定为今后的销售单价（同一组中的数据用该组区间的中点值作代表），结合你对（1）的判断，当月产量为12件时，预测当月的利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两个班级（各40名学生）进行一门考试，为易于统计分析，将甲、乙两个班学生的成绩分成如下四组：，，，，并分别绘制了如下的频率分布直方图：

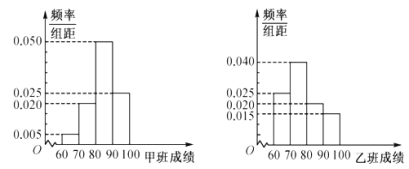
    规定：成绩不低于90分的为优秀，低于90分的为不优秀.

    （1）根据这次抽查的数据，填写下面的列联表：

    优秀

    不优秀

    合计

    甲班

    乙班

    合计

    （2）根据（1）中的列联表，能否有的把握认为成绩是否优秀与班级有关？

    附：临界值参考表与参考公式

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

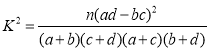    （，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业新研发了一种产品，产品的成本由原料成本及非原料成本组成.每件产品的非原料成本（元）与生产该产品的数量（千件）有关，经统计得到如下数据：

    x

    1

    2

    3

    4

    5

    6

    7

    8

    y

    112

    61

    44.5

    35

    30.5

    28

    25

    24

    根据以上数据，绘制了散点图.观察散点图，两个变量不具有线性相关关系，现考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合，已求得：用指数函数模型拟合的回归方程为，与的相关系数；，，，，，，（其中）；

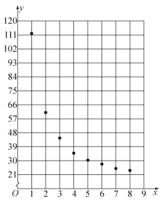
    （1）用反比例函数模型求关于的回归方程；

    （2）用相关系数判断上述两个模型哪一个拟合效果更好（精确到0.01），并用其估计产量为10千件时每件产品的非原料成本.

    参考数据：，

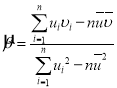    参考公式：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为：，，相关系数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， .

    （1）若存在极值点1，求的值；

    （2）若存在两个不同的零点，求证： （为自然对数的底数， ）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体中，AD⊥平面PDC，四边形ABCD为平行四边形，E为AD的中点，F为线段PB上的一点，∠CDP＝120°，AD＝3，AP＝5，．

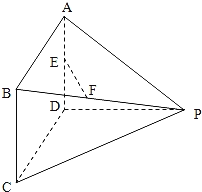
    （Ⅰ）试确定点F的位置，使得直线EF∥平面PDC；

    （Ⅱ）若PB＝3BF，求直线AF与平面PBC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，过点的直线l与抛物线交于A，B两点，以AB为直径作圆，记为,与抛物线C的准线始终相切.

    （1）求抛物线C的方程；

    （2）过圆心M作x轴垂线与抛物线相交于点N，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校高三年级为了解学生在家参加线上教学的学习情况，对高三年级进行了网上数学测试,他们的成绩在80分到150分之间,根据统计数据得到如下频率分布直方图：

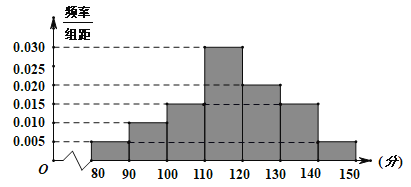
    若成绩在区左侧，认为该学生属于“网课潜能生”，成绩在区间之间，认为该学生属于“网课中等生”，成绩在区间右侧，认为该学生属于“网课优等生”．

    （1）若小明的测试成绩为100分，请判断小明是否属于“网课潜能生”，并说明理由：（参考数据：计算得）

    （2）该校利用分层抽样的方法从样本的，两组中抽出6人，进行教学反馈，并从这6人中再抽取2人，赠送一份学习资料，求获赠学习资料的2人中恰有1人成绩超过90分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：，分别是其左、右焦点，过的直线l与椭圆C交于A，B两点，且椭圆C的离心率为，的内切圆面积为，.

    （I）求椭圆C的方程；

    （II）若时，求直线l的方程

    查看答案和解析>>

    同步练习册答案