
ЁОЬтФПЁПМзЁЂввСНИіАрМЖЃЈИї40УћбЇЩњЃЉНјаавЛУХПМЪдЃЌЮЊвзгкЭГМЦЗжЮіЃЌНЋМзЁЂввСНИіАрбЇЩњЕФГЩМЈЗжГЩШчЯТЫФзщЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌВЂЗжБ№ЛцжЦСЫШчЯТЕФЦЕТЪЗжВМжБЗНЭМЃК
ЃЌВЂЗжБ№ЛцжЦСЫШчЯТЕФЦЕТЪЗжВМжБЗНЭМЃК
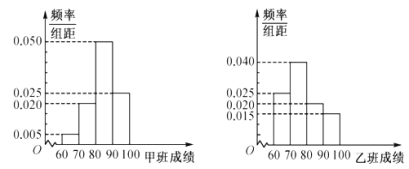
ЙцЖЈЃКГЩМЈВЛЕЭгк90ЗжЕФЮЊгХауЃЌЕЭгк90ЗжЕФЮЊВЛгХау.
ЃЈ1ЃЉИљОнетДЮГщВщЕФЪ§ОнЃЌЬюаДЯТУцЕФ![]() СаСЊБэЃК
СаСЊБэЃК
гХау | ВЛгХау | КЯМЦ | |
МзАр | |||
ввАр | |||
КЯМЦ |
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЕФСаСЊБэЃЌФмЗёга![]() ЕФАбЮеШЯЮЊГЩМЈЪЧЗёгХаугыАрМЖгаЙиЃП
ЕФАбЮеШЯЮЊГЩМЈЪЧЗёгХаугыАрМЖгаЙиЃП
ИНЃКСйНчжЕВЮПМБэгыВЮПМЙЋЪН
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЃЈ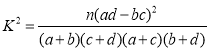 ЃЌЦфжа
ЃЌЦфжа![]() ЃЉ
ЃЉ
ЁОД№АИЁПЃЈ1ЃЉЬюБэМћНтЮіЃЛЃЈ2ЃЉУЛга![]() ЕФАбЮеШЯЮЊГЩМЈЪЧЗёгХаугыАрМЖгаЙи
ЕФАбЮеШЯЮЊГЩМЈЪЧЗёгХаугыАрМЖгаЙи
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМЧѓГіМзАрЁЂввАргХауЕФШЫЪ§МДПЩЃЛ
ЃЈ2ЃЉжБНгРћгУПЈЗНЙЋЪННсКЯСйНчжЕВЮПМБэМДПЩЕУЕНД№АИ.
ЃЈ1ЃЉгЩЬтвтЃЌМзАргХауЕФШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
ввАргХауЕФШЫЪ§ЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() СаСЊБэЃЌШчЯТЃК
СаСЊБэЃЌШчЯТЃК
гХау | ВЛгХау | КЯМЦ | |
МзАр | 10 | 30 | 40 |
ввАр | 6 | 34 | 40 |
КЯМЦ | 16 | 64 | 80 |
ЃЈ2ЃЉ![]() ЃЌ
ЃЌ
ЫљвдУЛга![]() ЕФАбЮеШЯЮЊГЩМЈЪЧЗёгХаугыАрМЖгаЙи.
ЕФАбЮеШЯЮЊГЩМЈЪЧЗёгХаугыАрМЖгаЙи.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=log4ЃЈ4x+1ЃЉ+kxгыgЃЈxЃЉ=log4ЃЈa2xЉ![]() aЃЉЃЌЦфжаfЃЈxЃЉЪЧХМКЏЪ§ЃЎ
aЃЉЃЌЦфжаfЃЈxЃЉЪЧХМКЏЪ§ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§kЕФжЕЃЛ
ЃЈ2ЃЉЧѓКЏЪ§gЃЈxЃЉЕФЖЈвхгђЃЛ
(3)ШєКЏЪ§fЃЈxЃЉгыgЃЈxЃЉЕФЭМЯѓгаЧвжЛгавЛИіЙЋЙВЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППеЦјжЪСПжИЪ§(Air Quality IndexЃЌМђГЦAQI)ЪЧЖЈСПУшЪіПеЦјжЪСПзДПіЕФжИЪ§ЃЌПеЦјжЪСПАДееAQIДѓаЁЗжЮЊСљМЖЃК0ЁЋ50ЮЊгХЃЛ51ЁЋ100ЮЊСМЃЛ101ЁЋ150ЮЊЧсЖШЮлШОЃЛ151ЁЋ200ЮЊжаЖШЮлШОЃЛ201ЁЋ300ЮЊжиЖШЮлШОЃЛ>300ЮЊбЯжиЮлШО.вЛЛЗБЃШЫЪПМЧТМСЫФГЕи2020ФъФГдТ10ЬьЕФAQIЕФОЅвЖЭМШчЭМЫљЪО.
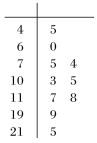
ЃЈ1ЃЉРћгУИУбљБОЙРМЦИУЕиБОдТПеЦјжЪСПгХСМ(AQIЁм100)ЕФЬьЪ§ЃЛ(АДетИідТзмЙВга30ЬьМЦЫу)
ЃЈ2ЃЉШєДгбљБОжаЕФПеЦјжЪСПВЛМб(AQI>100)ЕФетаЉЬьжаЃЌЫцЛњЕиГщШЁСНЬьЩюШыЗжЮіИїжжЮлШОжИБъЃЌЧѓИУСНЬьЕФПеЦјжЪСПЕШМЖЧЁКУВЛЭЌЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ 1ЃЌдкжБНЧЬнаЮ![]() жаЃЌ
жаЃЌ ![]() ЃЌЧв
ЃЌЧв![]() ЃЎЯжвд
ЃЎЯжвд![]() ЮЊвЛБпЯђЭтзїе§ЗНаЮ
ЮЊвЛБпЯђЭтзїе§ЗНаЮ![]() ЃЌШЛКѓбиБп
ЃЌШЛКѓбиБп![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЗелЃЌЪЙ
ЗелЃЌЪЙ![]() ЦНУцгыЦНУц
ЦНУцгыЦНУц![]() ДЙжБЃЌ
ДЙжБЃЌ ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌШчЭМ 2ЃЎ
ЕФжаЕуЃЌШчЭМ 2ЃЎ
ЃЈ1ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕга![]() ЃЌ
ЃЌ![]() СНИіЗжГЇЩњВњФГжжВњЦЗЃЌЙцЖЈИУВњЦЗЕФФГЯюжЪСПжИБъжЕВЛЕЭгк130ЕФЮЊгХжЪЦЗЃЎЗжБ№Дг
СНИіЗжГЇЩњВњФГжжВњЦЗЃЌЙцЖЈИУВњЦЗЕФФГЯюжЪСПжИБъжЕВЛЕЭгк130ЕФЮЊгХжЪЦЗЃЎЗжБ№Дг![]() ЃЌ
ЃЌ![]() СНГЇжаИїЫцЛњГщШЁ100МўВњЦЗЭГМЦЦфжЪСПжИБъжЕЃЌЕУЕНШчЭМЦЕТЪЗжВМжБЗНЭМЃК
СНГЇжаИїЫцЛњГщШЁ100МўВњЦЗЭГМЦЦфжЪСПжИБъжЕЃЌЕУЕНШчЭМЦЕТЪЗжВМжБЗНЭМЃК
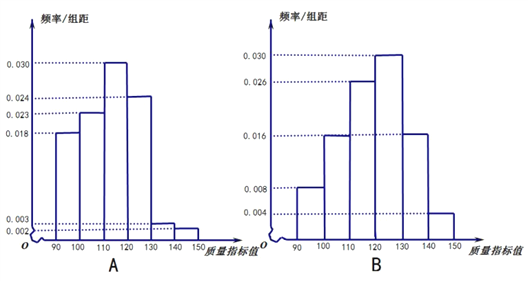
ЃЈ1ЃЉИљОнЦЕТЪЗжВМжБЗНЭМЃЌЗжБ№ЧѓГі![]() ЗжГЇЕФжЪСПжИБъжЕЕФжкЪ§КЭжаЮЛЪ§ЕФЙРМЦжЕЃЛ
ЗжГЇЕФжЪСПжИБъжЕЕФжкЪ§КЭжаЮЛЪ§ЕФЙРМЦжЕЃЛ
ЃЈ2ЃЉЬюаД![]() СаСЊБэЃЌВЂИљОнСаСЊБэХаЖЯЪЧЗёга
СаСЊБэЃЌВЂИљОнСаСЊБэХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊетСНИіЗжГЇЕФВњЦЗжЪСПгаВювьЃП
ЕФАбЮеШЯЮЊетСНИіЗжГЇЕФВњЦЗжЪСПгаВювьЃП
гХжЪЦЗ | ЗЧгХжЪЦЗ | КЯМЦ | |
| |||
| |||
КЯМЦ |
ЃЈ3ЃЉЃЈiЃЉДг![]() ЗжГЇЫљГщШЁЕФ100МўВњЦЗжаЃЌРћгУЗжВуГщбљЕФЗНЗЈГщШЁ10МўВњЦЗЃЌдйДгет10МўВњЦЗжаЫцЛњГщШЁ2МўЃЌвбжЊГщЕНвЛМўВњЦЗЪЧгХжЪЦЗЕФЬѕМўЯТЃЌЧѓГщШЁЕФСНМўВњЦЗЖМЪЧгХжЪЦЗЕФИХТЪЃЛ
ЗжГЇЫљГщШЁЕФ100МўВњЦЗжаЃЌРћгУЗжВуГщбљЕФЗНЗЈГщШЁ10МўВњЦЗЃЌдйДгет10МўВњЦЗжаЫцЛњГщШЁ2МўЃЌвбжЊГщЕНвЛМўВњЦЗЪЧгХжЪЦЗЕФЬѕМўЯТЃЌЧѓГщШЁЕФСНМўВњЦЗЖМЪЧгХжЪЦЗЕФИХТЪЃЛ
ЃЈiiЃЉНЋЦЕТЪЪгЮЊИХТЪЃЌДг![]() ЗжГЇжаЫцЛњГщШЁ10МўИУВњЦЗЃЌМЧГщЕНгХжЪЦЗЕФМўЪ§ЮЊ
ЗжГЇжаЫцЛњГщШЁ10МўИУВњЦЗЃЌМЧГщЕНгХжЪЦЗЕФМўЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЪ§бЇЦкЭћЃЎ
ЕФЪ§бЇЦкЭћЃЎ
ИНЃК![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЫФРтзЖ![]() жаЃЌЦНУц
жаЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкРт
дкРт![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() .
.

ЃЈЂёЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЕУЖўУцНЧ
ЃЌЪЙЕУЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ЃПШєДцдкЃЌЧѓГіЪЕЪ§
ЃПШєДцдкЃЌЧѓГіЪЕЪ§![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊЧњЯп
жаЃЌвбжЊЧњЯп![]() ЃК
ЃК![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌдквддЕу
ЮЊВЮЪ§ЃЉЃЌдквддЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂЕФМЋзјБъЯЕжаЃЌжБЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂЕФМЋзјБъЯЕжаЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭжБЯп
ЕФЦеЭЈЗНГЬКЭжБЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЧвгыжБЯп
ЧвгыжБЯп![]() ЦНааЕФжБЯп
ЦНааЕФжБЯп![]() НЛ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧѓЕу
СНЕуЃЌЧѓЕу![]() ЕН
ЕН![]() ЃЌ
ЃЌ![]() СНЕуЕФОрРыжЎЛ§.
СНЕуЕФОрРыжЎЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП[бЁао4ЁЊ4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ]
дкжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЎвдзјБъдЕуЮЊМЋЕуЃЌ
ЃЎвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШє![]() гы
гы![]() гаЧвНігаШ§ИіЙЋЙВЕуЃЌЧѓ
гаЧвНігаШ§ИіЙЋЙВЕуЃЌЧѓ![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж12ЗжЃЌЃЈ1ЃЉаЁЮЪ7ЗжЃЌЃЈ2ЃЉаЁЮЪ5ЗжЃЉ
ЩшКЏЪ§![]()
ЃЈ1ЃЉШє![]() дк
дк![]() ДІШЁЕУМЋжЕЃЌШЗЖЈ
ДІШЁЕУМЋжЕЃЌШЗЖЈ![]() ЕФжЕЃЌВЂЧѓДЫЪБЧњЯп
ЕФжЕЃЌВЂЧѓДЫЪБЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШє![]() дк
дк![]() ЩЯЮЊМѕКЏЪ§ЃЌЧѓ
ЩЯЮЊМѕКЏЪ§ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЁЃ
ЕФШЁжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com