
【题目】已知抛物线![]() 的焦点为F,点
的焦点为F,点![]() 在此抛物线上,
在此抛物线上,![]() ,不过原点的直线
,不过原点的直线![]() 与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
(1)求抛物线C的方程;
(2)证明:直线![]() 恒过定点;
恒过定点;
(3)若线段AB中点的纵坐标为2,求此时直线![]() 和圆M的方程.
和圆M的方程.
【答案】(1)![]() ;(2)定点
;(2)定点![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根据抛物线的定义,将![]() 转化为抛物线上的点
转化为抛物线上的点![]() 到准线的距离,从而求出
到准线的距离,从而求出![]() ,得到抛物线方程.
,得到抛物线方程.
(2)直线与抛物线联立,得到![]() ,然后利用以
,然后利用以![]() 为直径的圆
为直径的圆![]() 过坐标原点,即
过坐标原点,即![]() ,代入
,代入![]() ,求出斜率与截距的关系,得到直线过的定点.
,求出斜率与截距的关系,得到直线过的定点.
(3)根据![]() 中点坐标,求出直线的斜率,得到直线方程,再求出
中点坐标,求出直线的斜率,得到直线方程,再求出![]() 长度,即圆的半径,得到圆的方程.
长度,即圆的半径,得到圆的方程.
(1)抛物线![]() ,其准线为
,其准线为![]()
![]() 点
点![]() 在此抛物线上,
在此抛物线上,![]() ,
,
![]() 点
点![]() 到准线的距离等于
到准线的距离等于![]() ,即
,即![]() ,得
,得![]()
![]() 所求抛物线方程为
所求抛物线方程为![]()
(2)①当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,易知
,易知![]() .
.
联立方程组得![]() ,从而可得方程
,从而可得方程![]()
由题意可知![]()
![]()
所以![]()
因为以![]() 为直径的圆
为直径的圆![]() 过坐标原点,
过坐标原点,
所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() ,所以直线
,所以直线![]() 恒过定点
恒过定点![]() .
.
②当直线![]() 的斜率不存在时,易求得点
的斜率不存在时,易求得点![]() 坐标分别为
坐标分别为![]() ,
,![]() ,直线
,直线![]() 也过点
也过点![]() .
.
综合①②可知,直线![]() 恒过定点
恒过定点![]() .
.
(3)由题意可知直线![]() 斜率存在,设线段
斜率存在,设线段![]() 中点坐标为
中点坐标为![]()
由(2)中所得![]() ,
,
则![]()
所以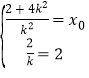 ,解得
,解得![]()
所以直线![]() 方程为
方程为![]() .
.
因为线段![]() 中点坐标为
中点坐标为![]() ,即为圆
,即为圆![]() 的圆心坐标,
的圆心坐标,
设圆![]()
![]() .
.
代入![]() ,得
,得![]()
所以圆![]() 的方程为
的方程为![]()


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】某小学为了解四年级学生的家庭作业用时情况,从本校四年级随机抽取了一批学生进行调查,并绘制了学生作业用时的频率分布直方图,如图所示.
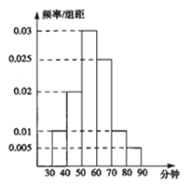
(1)估算这批学生的作业平均用时情况;
(2)作业用时不能完全反映学生学业负担情况,这与学生自身的学习习惯有很大关系如果用时四十分钟之内评价为优异,一个小时以上为一般,其它评价为良好.现从优异和良好的学生里面用分层抽样的方法抽取300人,其中女生有90人(优异20人).请完成列联表,并根据列联表分析能否在犯错误的概率不超过0.05的前提下认为学习习惯与性别有关系?
男生 | 女生 | 合计 | |
良好 | |||
优异 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各![]() 名,将男性、女性使用微信的时间分成
名,将男性、女性使用微信的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

(1)根据女性频率分布直方图,估计女性使用微信的平均时间;
(2)若每天玩微信超过![]() 小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成
小时的用户列为“微信控”,否则称其为“非微信控”,请你根据已知条件完成![]() 的列联表,并判断是否有
的列联表,并判断是否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )
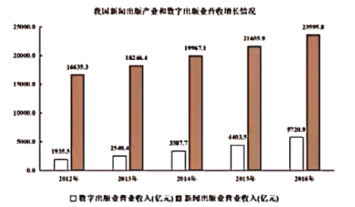
A. 2012年至2016年我国新闻出版业和数字出版业营收均逐年增加
B. 2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍
C. 2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍
D. 2016年我国数字出版营收占新闻出版营收的比例未超过三分之一
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作直线
作直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,过
,过![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() ,若
,若![]() ,则点
,则点![]() 的横坐标为__________,
的横坐标为__________,![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值,并求取得最大值时直线
的面积之差的绝对值的最大值,并求取得最大值时直线![]() 的方程.
的方程.![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面ABCD是边长为3的正方形,EFG分别是棱ABPBPC的中点,
,底面ABCD是边长为3的正方形,EFG分别是棱ABPBPC的中点,![]() ,
,![]() .
.

(Ⅰ)求证:平面EFG∥平面PAD;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com