
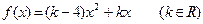 ,对任意实数
,对任意实数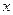 ,有
,有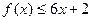 恒成立;数列
恒成立;数列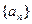 满足
满足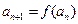 .
.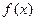 的解析式和值域;
的解析式和值域;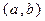 ,使得当
,使得当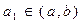 时,数列
时,数列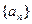 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;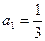 ,是否存在非零整数
,是否存在非零整数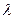 ,使得对任意
,使得对任意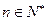 ,都有
,都有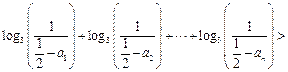
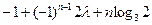 恒成立,若存在,
恒成立,若存在,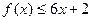 恒成立等价于
恒成立等价于 恒成立,…1分
恒成立,…1分 ,化简得
,化简得 ,从而得
,从而得 ,
, ,………3分
,………3分 .…………………4分
.…………………4分 时,数列
时,数列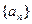 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下: ,则
,则 ,
, ,均有
,均有 ;………………7分
;………………7分

 ,即
,即 ,所以数列
,所以数列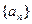 在区间
在区间 上是递增数列…10分
上是递增数列…10分 、
、 、
、 等无穷多个.
等无穷多个.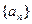 在某个区间上是递增数列,则
在某个区间上是递增数列,则

 …7分
…7分 时,
时, ,
, ,均有
,均有 且
且 ,
,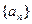 在区间
在区间 上是递增数列.…………………………10分
上是递增数列.…………………………10分 ,从而
,从而 ;
; ,
, ; ………12分
; ………12分 ,则有
,则有 且
且 ;
; ,可得
,可得 ,
, 是以
是以 为首项,公比为
为首项,公比为 的等比数列,………14分
的等比数列,………14分 ,即
,即 ,
, ,
, ,∴
,∴ , …16分
, …16分
 . ………………………18分
. ………………………18分 ,从而
,从而 ;
; ,
, ;………12分
;………12分 ,则有
,则有 且
且 ;
; ,可得
,可得 ,所以数列
,所以数列 是
是 为首项,公比为
为首项,公比为 的等比数列,…………………14分
的等比数列,…………………14分 ,即
,即 ,
, ,
, ,所以
,所以 ,
,
 .………………………16分
.………………………16分

 ,所以,
,所以, 恒成立
恒成立 恒成立,当且仅当
恒成立,当且仅当 时,
时, 有最小值
有最小值 为。
为。
 恒成立,当且仅当
恒成立,当且仅当 时,有最大值
时,有最大值 为。
为。
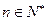 ,有
,有 。又
。又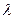 非零整数,
非零整数, …………18分
…………18分

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源:不详 题型:填空题
 的图象与函数g(x)的
的图象与函数g(x)的 图象关于直线
图象关于直线 对称,令
对称,令 则关于函数
则关于函数 有下列命题 ( )
有下列命题 ( )  的图象关于原点对称;②
的图象关于原点对称;② 为偶函数;
为偶函数; 的最小值为0; ④
的最小值为0; ④ 在(0,1)上为减函数
在(0,1)上为减函数查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com