
【题目】为了了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验将![]() 只小鼠随机分成
只小鼠随机分成![]() 、
、![]() 两组,每组
两组,每组![]() 只,其中
只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:
组小鼠给服乙离子溶液每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比根据试验数据分别得到如图所示的直方图:


根据频率分布直方图估计,事件![]() :“乙离子残留在体内的百分比不高于
:“乙离子残留在体内的百分比不高于![]() ”发生的概率
”发生的概率![]() .
.
(1)根据所给的频率分布直方图估计各段频数;
(附:频数分布表)
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
(2)请估计甲离子残留百分比的中位数,请估计乙离子残留百分比的平均值.
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 所经过的定点
所经过的定点![]() 恰好是椭圆
恰好是椭圆![]() 的一个焦点,且椭圆
的一个焦点,且椭圆![]() 上的点到点
上的点到点![]() 的最大距离为
的最大距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,直线
,直线![]() .试证:当点
.试证:当点![]() 在椭圆
在椭圆![]() 上运动时,直线
上运动时,直线![]() 与圆
与圆![]() 恒相交,并求直线
恒相交,并求直线![]() 被圆
被圆![]() 所截得弦长
所截得弦长![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本![]() 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为![]() 元.
元.
(Ⅰ)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数(利润=总售价-成本-促销费);
万元的函数(利润=总售价-成本-促销费);
(Ⅱ)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛,图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
(1)完成下列![]() 的列联表,并回答是否有
的列联表,并回答是否有![]() 的把握认为“两个学段的学生对四大名著的了解有差异”?
的把握认为“两个学段的学生对四大名著的了解有差异”?
成绩小于60分的人数 | 成绩不小于60的人数 | 合计 | |
初中年级 | |||
高中年级 | |||
合计 |
(2)规定竞赛成绩不少于70分的为优秀,按分层抽样的方法从高中,初中年级优秀学生中抽取5人进行复赛,在复赛人员中选3人进行面试,记面试人员中来自初中段的为随机变量X,求随机变量X的分布列与期望.
![]() 其中
其中![]()
附表:
| 0.10 | 0.05 | span>0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生![]() 人,学校团委为了了解本校学生到上述红色基地硏学旅行的情况,随机调查了
人,学校团委为了了解本校学生到上述红色基地硏学旅行的情况,随机调查了![]() 名学生,其中到过中共一大会址或井冈山研学旅行的共有
名学生,其中到过中共一大会址或井冈山研学旅行的共有![]() 人,到过井冈山研学旅行的
人,到过井冈山研学旅行的![]() 人,到过中共一大会址并且到过井冈山研学旅行的恰有
人,到过中共一大会址并且到过井冈山研学旅行的恰有![]() 人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有( )人
人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有( )人
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
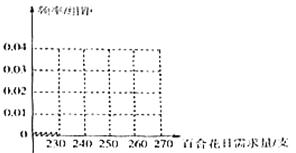
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】同学们刚刚结束了史上最长寒假,经高二各班数学老师了解,同学们每天沉迷于学习中不能自拔,每天认真完成作业,作业正确率很高,为同学们点赞!某个周日一位同学正在三河滩锻炼身体,突然接到级部通知回家开网络学生会,从三河滩某处A到对岸公路BC的距离AB为2km, B处与家C间的距离为4km,从A到C,必须先步行到BC上的某一点D,步行速度为5km/h,再乘电动车到C,电动车车速为10km/h,记![]()
(1)试将由A到C所用的时间t表示为![]() 的函数
的函数![]() ;
;
(2)间![]() 为多少时,由A到C所用的时间t最少?
为多少时,由A到C所用的时间t最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
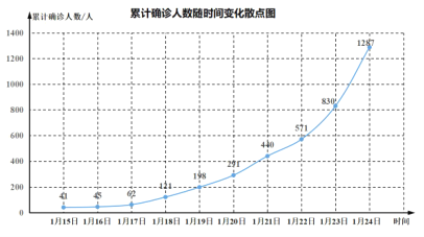
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为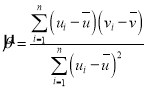 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com