解:(1)f'(x)=ax
2+2bx+c,由题意及导数的几何意义得
f'(1)=a+2b+c=0①f'(m)=am
2+2bm+c=-a②
又a<b<c,可得3a<a+2b+c<3c,即3a<0<3c,故a<0,c>0,
由①得c=-a-2b,代入a<b<c,再由a<0,得

③
将c=-a-2b代入②得am
2+2bm-2b=0,即方程ax
2+2bx-2b=0有实根.
故其判别式△=4b
2+8ab≥0得
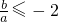
,或

④
由③,④得

;
(2)由f'(x)=ax
2+2bx+c的判别式△'=4b
2-4ac>0,
知方程f'(x)=ax
2+2bx+c=0(*)有两个不等实根,设为x
1,x
2,
又由f'(1)=a+2b+c=0知,x
1=1为方程(*)的一个实根,则有根与系数的关系得
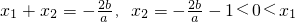
,
当x<x
2或x>x
1时,f'(x)<0,当x
2<x<x
1时,f'(x)>0,
故函数f(x)的递增区间为[x
2,x
1],由题设知[x
2,x
1]=[s,t],
因此

,由(Ⅰ)知

得|s-t|的取值范围为[2,4);
(3)由f'(x)+a<0,即ax
2+2bx+a+c<0,即ax
2+2bx-2b<0,
因为a<0,则

,整理得

,
设
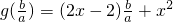
,可以看作是关于

的一次函数,由题意
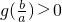
对于

恒成立,
故

即

得

或

,
由题意,

,
故

,因此k的最小值为

.
分析:(1)利用函数图象在A,B两点处的切线的斜率,可以得到f'(1)=0,f'(m)=-a,然后利用a,b,c的大小关系,确定a,c的符号,通过消元得到am
2+2bm-2b=0,利用二次方程的根的情况,可得

,
(2)由导数的符号确定函数的单调增区间,利用二次方程根与系数的关系得到|s-t|关于a,b的关系式,即可得|s-t|的取值范围;(3)由f'(x)+a<0得ax
2+2bx-2b<0,通过转换主元,利用不等式恒成立的条件得到x的范围,从而得到k的范围.
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间,掌握不等式恒成立时所取的条件.是个难题.是个难题.

 ax3+bx2+cx(a<b<c),其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a.
ax3+bx2+cx(a<b<c),其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a. ;
; ③
③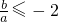 ,或
,或 ④
④ ;
;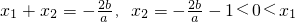 ,
, ,由(Ⅰ)知
,由(Ⅰ)知 得|s-t|的取值范围为[2,4);
得|s-t|的取值范围为[2,4); ,整理得
,整理得 ,
,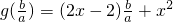 ,可以看作是关于
,可以看作是关于 的一次函数,由题意
的一次函数,由题意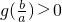 对于
对于 恒成立,
恒成立, 即
即
 或
或 ,
, ,
, ,因此k的最小值为
,因此k的最小值为 .
. ,
,

 设函数f(x)=(a
设函数f(x)=(a