
分析 (Ⅰ)求导数,利用曲线y=f(x)在点(1,f(1))处的切线方程为y=$\frac{1}{2}$x+b,可求a、b的值;
(Ⅱ)确定函数的单调性,即可求f(x)的极值.
解答 解:(Ⅰ)由$f'(x)=\frac{a}{x}-\frac{3}{2}$,则$f'(1)=a-\frac{3}{2}=\frac{1}{2}$,得a=2,
所以$f(x)=2lnx-\frac{3}{2}x+3$,$f(1)=\frac{3}{2}$,
把切点$(1,\frac{3}{2})$代入切线方程有$\frac{3}{2}=\frac{1}{2}+b$,解得b=1,
综上:a=2,b=1.(6分)
(Ⅱ)由(Ⅰ)有$f'(x)=\frac{2}{x}-\frac{3}{2}=\frac{4-3x}{2x}$,
当0<x<$\frac{4}{3}$时,f'(x)>0,f(x)单调递增;当$x>\frac{4}{3}$时,f'(x)<0,f(x)单调递减.
所以f(x)在$x=\frac{4}{3}$时取得极大值$f(\frac{4}{3})=2ln\frac{4}{3}+1$,f(x)无极小值.(12分)
点评 本题考查导数知识的运用,考查导数的几何意义与极值,考查函数的单调性,正确求导是关键.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2n-1)2-1=4n2-4n | B. | (3n-1)2-1=9n2-6n | C. | (2n+1)2-1=4n2+4n | D. | (3n+1)2-1=9n2+6n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
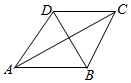 如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).
如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2\sqrt{2},+∞)$ | B. | $(4-2\sqrt{2},+∞)$ | C. | (4,+∞) | D. | $(4+2\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com