
【题目】已知两个函数f(x)=log4(a ![]() )(a≠0),g(x)=log4(4x+1)﹣
)(a≠0),g(x)=log4(4x+1)﹣ ![]() 的图象有且只有一个公共点,则实数a的取值范围是 .
的图象有且只有一个公共点,则实数a的取值范围是 .
【答案】{a,a>1或a=﹣3}
【解析】g(x)=log4(a2x﹣ ![]() a),
a),
函数f(x)与g(x)的图象有且只有一个公共点,即
方程f(x)=g(x)只有一个解
由已知得log4(4x+1) ![]() x=log4(a2x﹣
x=log4(a2x﹣ ![]() a),
a),
∴log4( ![]() )=log4(a2x﹣
)=log4(a2x﹣ ![]() a),
a),
方程等价于 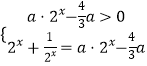 ,
,
设2x=t,t>0,则(a﹣1)t2﹣ ![]() at﹣1=0有一解
at﹣1=0有一解
若a﹣1>0,设h(t)=(a﹣1)t2﹣ ![]() at﹣1,
at﹣1,
∵h(0)=﹣1<0,∴恰好有一正解
∴a>1满足题意
若a﹣1=0,即a=1时,h(t)=﹣ ![]() ﹣1,由h(t)=0,得t=﹣
﹣1,由h(t)=0,得t=﹣ ![]() <0,不满足题意
<0,不满足题意
若a﹣1<0,即a<1时,由△=(﹣ ![]() )2﹣4(a﹣1)×(﹣1)=0,得a=﹣3或a=
)2﹣4(a﹣1)×(﹣1)=0,得a=﹣3或a= ![]() ,
,
当a=﹣3时,t= ![]() 满足题意
满足题意
当a= ![]() 时,t=﹣2(舍去)
时,t=﹣2(舍去)
综上所述实数a的取值范围是{a|a>1或a=﹣3}.
所以答案是:{a|a>1或a=﹣3}.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】将直线2x﹣y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x﹣4y=0相切,则实数λ的值为( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(k﹣2)x2+2kx﹣3. (Ⅰ)当k=4时,求f(x)在区间(﹣4,1)上的值域;
(Ⅱ)若函数f(x)在(0,+∞)上至少有一个零点,求实数k的取值范围;
(Ⅲ)若f(x)在区间[1,2]上单调递增,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形CDEF中,DE=CD= ![]() ,EF=2+
,EF=2+ ![]() ,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E﹣ABCD(E,F重合).
,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E﹣ABCD(E,F重合). 
(1)求证:BE⊥DE;
(2)设点M为线段AB的中点,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时, f(x)= ![]() ,
,
则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.1﹣2a
B.2a﹣1
C.1﹣2﹣a
D.2﹣a﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有老、中、青教职工215人,其中青年教职工80人,中年教职工人数是老年教职工人数的2倍.为了解教职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工16人,则该样本中的老年教职工人数为( )
A.6
B.8
C.9
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,点E是棱PA的中点,PB=PD,平面BDE⊥平面ABCD. 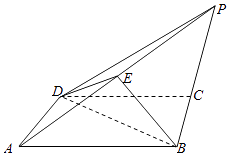
(Ⅰ)求证:PC∥平面BDE;
(Ⅱ)求证:PC⊥平面ABCD;
(Ⅲ)设PC=λAB,试判断平面PAD⊥平面PAB能否成立;若成立,写出λ的一个值(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com