
【题目】如图,在△ABC中, ![]() ,
, ![]()

(1)用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(2)若 ![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
(3)若 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:因为 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,
,
(2)证明:因为 ![]() ,所以
,所以 ![]() ,即
,即 ![]() ,
,
即 ![]() ,又因为
,又因为 ![]() ,
,
所以 ![]() ,即
,即 ![]() .
.
所以 ![]() ,所以
,所以 ![]() ,
,
(3)解:因为 ![]() ,所以
,所以 ![]() ,
,
即 ![]() ,因此
,因此 ![]() ,
,
同理 ![]() ,又
,又 ![]() ,所以
,所以 ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
即 ![]() ①
①
又因为 ![]() ,
, ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
即 ![]() ②
②
由①②得 ![]() .
.
【解析】(1)根据向量的加减的几何意义即可求出,(2)根据向量的模和向量的垂直的条件即可判断,(3)根据向量的加减的几何意义和向量的数量积的运算即可求出
【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案,需要熟知如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点. 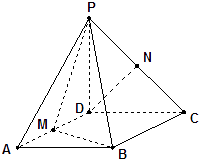
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)求点A到平面PMB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆两焦点 ![]() ,并且经过点
,并且经过点 ![]() .
.
(1)求椭圆的方程;
(2)若过点A(0,2)的直线l与椭圆交于不同的两点M、N(M在A、N之间),试求△OAM与△OAN面积之比的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=g(x),y=f(x)的解析式;
(2)若h(x)=f(x)+a在(﹣1,1)上有零点,求a的取值范围;
(3)若对任意的t∈(﹣4,4),不等式f(6t﹣3)+f(t2﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() 是奇函数.
是奇函数.
(1)若点Q(1,3)在函数f(x)的图象上,求函数f(x)的解析式;
(2)写出函数f(x)的单调区间(不要解答过程,只写结果);
(3)设点A(t,0),B(t+1,0)(t∈R),点P在f(x)的图象上,且△ABP的面积为2,若这样的点P恰好有4个,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC= ![]() AD=2,AC平分∠BAD.
AD=2,AC平分∠BAD. 
(1)求证:CE∥平面OAB;
(2)求四面体OACE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n次多项式 ![]() ,在求fn(x0)值的时候,不同的算法需要进行的运算次数是不同的.例如计算
,在求fn(x0)值的时候,不同的算法需要进行的运算次数是不同的.例如计算 ![]() (k=2,3,4,…,n)的值需要k﹣1次乘法运算,按这种算法进行计算f3(x0)的值共需要9次运算(6次乘法运算,3次加法运算).现按如图所示的框图进行运算,计算fn(x0)的值共需要次运算.( )
(k=2,3,4,…,n)的值需要k﹣1次乘法运算,按这种算法进行计算f3(x0)的值共需要9次运算(6次乘法运算,3次加法运算).现按如图所示的框图进行运算,计算fn(x0)的值共需要次运算.( ) 
A.2n
B.2n
C.![]()
D.n+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com