
(本小题满分12分)某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示. 质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
(1)这6件样品中来自A、B、C各车间产品的数量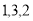 ;(2)
;(2)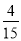
【解析】
试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(3)注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的,两者都是等可能性.(4)在几何概型中注意区域是线段,平面图形,立体图形.
试题解析:(1)因为样本容量与总体中的个体数的比是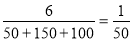 ,(2分)
,(2分)
所以A车间产品被选取的件数为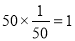 , (3分)
, (3分)
B车间产品被选取的件数为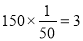 , (4分)
, (4分)
C车间产品被选取的件数为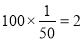 . (5分)
. (5分)
(2)设6件来自A、B、C三个车间的样品分别为:A;B1,B2,B3;C1,C2.
则从6件样品中抽取的这2件产品构成的所有基本事件为:(A,B1),(A,B2),(A,B3),(A,C1),(A,C2),(B1,B2),(B1,B3),(B1,C1),(B1,C2),(B2,B3),(B2,C1),(B2,C2),(B3,C1),(B3,C2),(C1,C2),共15个. (8分)
每个样品被抽到的机会均等,因此这些基本事件的出现是等可能的. 记事件D:“抽取的这2件产品来自相同车间”,则事件D包含的基本事件有:(B1,B2),(B1,B3),(B2,B3),(C1,C2),共4个.
所以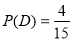 ,即这2件产品来自相同车间的概率为
,即这2件产品来自相同车间的概率为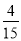 . (12分)
. (12分)
考点:1、分层抽样的应用;2、利用古典概型求随机事件的概率.


科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考文科数学试卷(解析版) 题型:选择题
一枚硬币连掷2次,只有一次出现正面的概率为( )
A.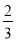 B.
B.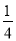 C.
C.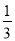 D.
D.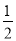
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考理科数学试卷(解析版) 题型:选择题
已知双曲线的中心在原点,一个焦点为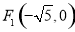 ,点
,点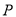 在双曲线上,且线段
在双曲线上,且线段 的中点坐标为
的中点坐标为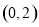 ,则此双曲线的方程是( )
,则此双曲线的方程是( )
A.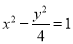 B.
B.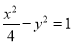 C.
C.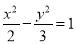 D.
D.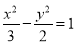
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:解答题
(本小题满分14分)设a为常数,且 .
.
(1)解关于x的不等式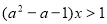 ;
;
(2)解关于x的不等式组 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:选择题
设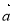 ,
,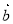 为非零向量,
为非零向量,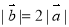 ,两组向量
,两组向量 和
和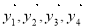 均由2个
均由2个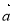 和2个
和2个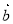 排列而成. 若
排列而成. 若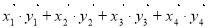 所有可能取值中的最小值为
所有可能取值中的最小值为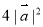 ,则
,则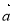 与
与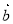 的夹角为
的夹角为
A.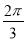 B.
B.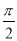 C.
C.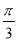 D.
D.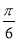
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测理科数学试卷(解析版) 题型:选择题
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为

A.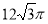 B.
B.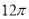 C.
C.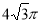 D.
D.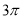
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考理科数学试卷(解析版) 题型:选择题
某同学在研究函数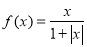 (
(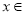 R)时,分别给出下面几个结论:
R)时,分别给出下面几个结论:
①等式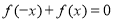 在
在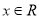 时恒成立;
时恒成立;
②函数 f (x)的值域为 (-1,1);
③若x1≠x2,则一定有f (x1)≠f (x2);
④函数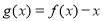 在
在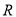 上有三个零点.
上有三个零点.
其中正确结论的序号是( )
A.①② B.①②③ C.①③④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com