
分析 ①利用导数判断在(0,e)递增,(e,+∞)递减得出f(3)>f(5),运用作差判断f(2)-f(5),f(2)-f(3)即可得出大小.
②构造函数ln(g(x))=$\frac{1}{x}$lnx(x>0),令h(x)=$\frac{1}{x}$lnx(x>0),运用导数求解极大值,得出h(x)的极大值为h(e)=$\frac{1}{e}$lne=$\frac{1}{e}$,结合对数求解即可.
解答 解:①∵函数f(x)=$\frac{lnx}{x}$,
∴f′(x)=$\frac{1-lnx}{{x}^{2}}$,
f′(x)=$\frac{1-lnx}{{x}^{2}}$=0,x=e,
f′(x)=$\frac{1-lnx}{{x}^{2}}$,>0,x∈(0,e)
f′(x)=$\frac{1-lnx}{{x}^{2}}$<0,x∈(e,+∞)
∴在(0,e)递增,(e,+∞)递减
∴f(3)>f(5),
∵f(2)-f(5)=$\frac{ln2}{2}$$-\frac{ln5}{5}$=$\frac{5ln2-2ln5}{10}$=$\frac{ln32-ln25}{10}$>0
∴f(2)>f(5)
∵f(2)-f(3)=$\frac{3ln2-2ln3}{6}$=$\frac{ln8-ln9}{6}$<0
∴f(3)>f(2)
故答案:f(5)<f(2)<f(3);
②∵函数g(x)=${x}^{\frac{1}{x}}$(x>0),
∴ln(g(x))=$\frac{1}{x}$lnx(x>0)
令h(x)=$\frac{1}{x}$lnx(x>0),
h′(x)=$\frac{1}{{x}^{2}}$(1-lnx)=0,x=e
h′(x)=$\frac{1}{{x}^{2}}$(1-lnx)<0,x>e
h′(x)=$\frac{1}{{x}^{2}}$(1-lnx)>0,0<x<e
∴h(x)=$\frac{1}{x}$lnx(x>0),
在(0,e)递增,在(e,+∞)递减,
h(x)的极大值为h(e)=$\frac{1}{e}$lne=$\frac{1}{e}$,
∴函数g(x)=${x}^{\frac{1}{x}}$(x>0)的最大值为e${\;}^{\frac{1}{e}}$,
故答案为:e${\;}^{\frac{1}{e}}$
点评 本题综合考察了学生运用导数解决问题的能力,构造思想,不等式的运用,对数的运用,属于比较新颖的题目.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 50m | B. | 100m | C. | 120m | D. | 150m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
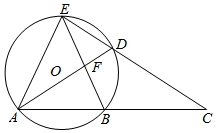 如图,点A、B、D、E在⊙O上,ED、AB的延长线交于点C,AD、BE交于点F,AE=EB=BC.
如图,点A、B、D、E在⊙O上,ED、AB的延长线交于点C,AD、BE交于点F,AE=EB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在圆柱OO1中,AB,CD是底面圆O的两条直径,CC1,DD1是圆柱OO1的两条母线,且AC=1,BC=CC1=$\sqrt{3}$.
如图所示,在圆柱OO1中,AB,CD是底面圆O的两条直径,CC1,DD1是圆柱OO1的两条母线,且AC=1,BC=CC1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com