
一个均匀的正四面体面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为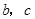 .
.
(1)记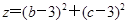 ,求
,求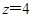 的概率;
的概率;
(2)若方程 至少有一根
至少有一根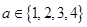 ,就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.
,就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.
(1) 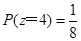 ;(2)
;(2)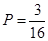 .
.
解析试题分析:(1)由于要将均匀的面上分别涂有1、2、3、4四个数字的正四面体随机投掷两次,故基本事件共有4×4=16个,然后求出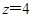 时,基本事件的个数,代入古典概型公式即可得到结果;(2)分类讨论方程根分别为1,2,3,5时,基本事件的个数,然后代入古典概型公式即可得到结果.
时,基本事件的个数,代入古典概型公式即可得到结果;(2)分类讨论方程根分别为1,2,3,5时,基本事件的个数,然后代入古典概型公式即可得到结果.
(1)因为是投掷两次,因此基本事件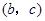 共有16个,
共有16个,
当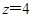 时,
时,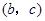 的所有取值为(1,3),(3,1),
的所有取值为(1,3),(3,1),
所以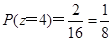 .
.
(2)①若方程一根为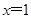 ,则
,则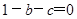 ,即
,即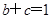 ,不成立.
,不成立.
②若方程一根为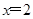 ,则
,则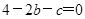 ,即
,即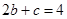 ,所以
,所以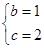 .
.
③若方程一根为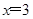 ,则
,则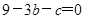 ,即
,即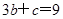 ,所以
,所以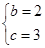 .
.
④若方程一根为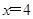 ,则
,则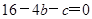 ,即
,即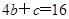 ,所以
,所以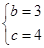 .
.
综合①②③④知,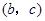 的所有可能取值为(1,2),(2,3), (3,4),所以,“漂亮方程”共有3个,方程为“漂亮方程”的概率为
的所有可能取值为(1,2),(2,3), (3,4),所以,“漂亮方程”共有3个,方程为“漂亮方程”的概率为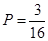 .
.
考点:1.创新能力;2.古典概型.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为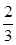 ,乙获胜的概率为
,乙获胜的概率为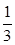 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
求甲在4局以内(含4局)赢得比赛的概率;
记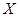 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求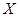 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校在一次运动会上,将要进行甲、乙两名同学的乒乓球冠亚军决赛,比赛实行三局两胜制.已知每局比赛中,若甲先发球,其获胜的概率为 ,否则其获胜的概率为
,否则其获胜的概率为 .
.
(1)若在第一局比赛中采用掷硬币的方式决定谁先发球,试求甲在此局获胜的概率;
(2)若第一局由乙先发球,以后每局由负方先发球.规定胜一局记2分,负一局记0分,记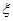 为比赛结束时甲的得分,求随机变量
为比赛结束时甲的得分,求随机变量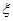 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于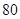 分的次数为
分的次数为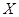 ,求
,求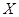 的分布列和数学期望
的分布列和数学期望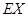 ..
..
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一袋中装有4个形状、大小完全相同的球,其中黑球2个,白球2个,假设每个小球从袋中被取出的可能性相同,首相由甲取出2个球,并不在将他们原袋中,然后由乙取出剩下的2个球.规定取出一个黑球记1分,取出一个白球记2分,取出球的总积分多者获胜.
(1)求甲、乙平局的概率;
(2)假设可以选择取球的先后顺序,应选择先取,还是后取,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料,若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2 800元,否则月工资定为2100元,令X表示此人选对A饮料的杯数,假设此人对A和B两种饮料没有鉴别能力.
(1)求X的分布列:
(2)求此员工月工资的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: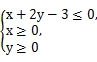 所表示的平面区域内的概率.
所表示的平面区域内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为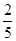 ,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com